用AP统计学知识点，揭秘“十赌九输”的真相！-AP统计学大数定律以及概率相关知识点

众所周知，博彩在中国大陆是被明令禁止的。其原因大家也可想而知，许多人因为赌博而输的倾家荡产、家破人亡。可是在许多国家和地区，赌场是个合法开放的场所，这就让很多在外旅游或者留学的人们想要进去看一看。

不过，进去看一看是可以的，一旦开始了这场“游戏”，那么后果可就是非常严重的了。今天这篇文章就要利用AP统计当中大数定律以及概率相关知识点来解释一下为什么会出现“十赌九输“这个现象。

理想化模型下的概率证明

首先我们假设一个看起来最公平的游戏方式。比如说摇6面骰子比大小的游戏。你拿一块钱和庄家比大小，赢了庄家给你一块钱，输了你给庄家一块钱。假设全程大家都不作弊，再不加倍的情况下，你和庄家赢钱的概率都是1/2.

假设你有n元的本金（n大于0） P（n）定义成你输掉全部本金的概率（也就是资金从n变成0） p（0）=1，因为当本金n变成0就无法继续参与游戏了。

接下来我们就会知道，假设每次游戏你拿出1块钱，那么你有1/2的机会赢，也就是现在手中资金是n+1，反之有一半的机会变成n-1。所以说

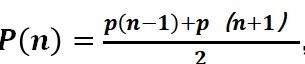输光n元的概率是输光n-1和输光n+1概率加和的一半（因为输和赢的机会都是1/2）

接着对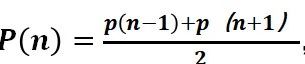

进行简单的变形，p(n+1) = 2 * p(n) - p(n-1)。设p(1)的值为a (也就是1元本金输光的概率，注意a不是1/2哦，因为1元本金可以先赢几场然后再输光。而不是第一把就输掉的概率)。显然0< a<=1。利用p(n+1) = 2 * p(n)-p(n-1)，得：

p(1) = a p(2) = 2a - 1 p(3) = 2(2a-1) - a = 3a - 2 p(4) = 4a - 3 ... p(n) = na - n + 1=n（a-1）+1

再次强调p（n）是概率，因此它一定是在0和1之间的（可以等于0，可以小于0），接下来我们来看：

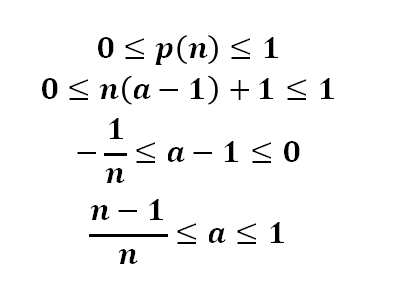我们会发现当本金越多，也就是n越大的时候，a会无限接近于1.（因为

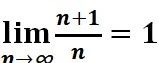，根据微积分当中的三明治定理可知，a的极限也是1）所以我们证明了p(1) 约等于1. 同样的过程可以得到p(2)约等于1, ...,一直下去，p(n) 约等于 1，也就是赌徒资金变为0的概率为1。那么上面的证明也仅仅证明了当这个游戏绝对公平，没有人作弊且玩家不加注的情况。但是在现实生活中的游戏完全没有这么理想化，具体见下方，我把真正生活中会出现的三种不公平的场景一一列举，分别是：游戏不绝对公平、玩家加注以及赌场出老千。

实际场景

庄家作弊

庄家作弊就不用说了，完全违背了随机的原则，那么庄家想让你输你就输掉了。这一点不过多讨论。

游戏并非绝对公平

不公平的意思也就指的是每一把游戏的胜率不是0.5，可能是0.49或者0.48。 以0.49为例那么继续用上面的证明来看，p（n）就不再是

，而是0.49P（n+1）+0.51P（n-1），p（n-1）一定会大于p（n+1）（当然是输光n-1元的更容易啦）也就是说p（n），即输光n元本金的概率就会加大。所以最后玩家还是会输光所有的钱，并且输的更快。那么看到这里有同学就会好奇，那赌场把游戏胜率设置的不公平哪里还会有人玩呢？事实上，仅仅1%的胜率区别在实操过程中根本难以发现。再加上周围环境的影响导致人不可能在灯红酒绿的地方冷静思考，自然庄家这个小把戏就不会被发现了。

玩家加注

玩家加注实际上是最可怕的一种情况，赌场里面有一句非常常见的话叫做“赢了就收手，输了就加倍”，简单解释一下就是假设你第一把下注2元，如果输了不要停止，下一把加注4元，意思是第二把如果赢了就可以把第一场本金赚回来了。假设你有1000块钱，第一把下注2，第二把4，第三把8，第四把16，第五把32，第六把64，第七把128，第8把256，第9把512.注意到后面你已经没有钱了，所以你即使有1000块钱，也会在第9把全部输掉。就算在其中某一把你赢了，也才只赢了2元（大家可以试着计算一下、假设第6把赢了，收益是64-32-16-8-4-2=2），这远远小于你投入的钱。而且如果你在其中赢了一把你还会继续去加倍么？答案是一定不会，因为人本身就是趋利避害的，当你某一次赢了之后是不可能把既得利益都押出去的，一定会收手。但是当你输的时候你会觉得输掉的都是自己的血汗钱，一步步增大赌注，最终陷进去。

大数定律

其次，庄家的钱远比你多得多，和你相比，庄家的钱就是无穷多的。他有钱赔，但你却没有钱输。并且实际上你赢钱的概率不一定是1/2，但庄家赢的概率一定是1/2. 我们用概率论当中大数定律的知识点来去看一下。 大数定律的定义：在随机试验中，每次出现的结果不同，但是大量重复实验出现的某个特定结果的比例一定接近于某一个确定的值。比如说投硬币投到正面的比例，见下图

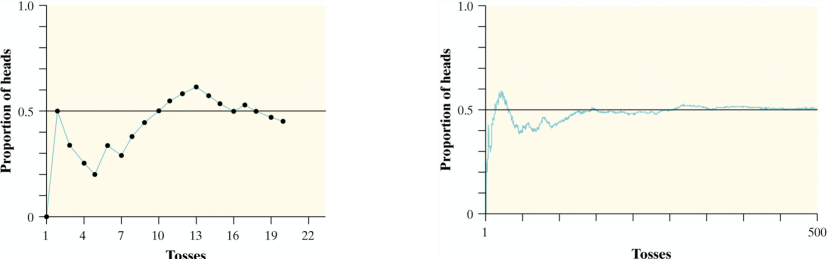也就是说当你仅仅玩两三把游戏的话，事实上你赢钱的机会并不是1/2，而是及其随机的。而每天光顾赌场的人很多，每个人都玩几把，对于庄家来说相当于他就玩了无数多场了。所以赌场的胜率是1/2，而你不是。 刚刚说的这一切都是建立在公平的基础上（赌场作弊除外），然而这种场景非常理想，如果是线上博彩，庄家可以随机操纵数据，让你输的血本无归。所以，永远不要尝试去碰赌博，不要和人性作对，因为人永远战胜不了自己的贪婪。