确实对于AP微积分的知识体系而言，同学们想要完全理解泰勒级数是比较困难的。因为我们缺少诸多的证明手段以致于这部分知识出现的时候会感觉到非常地突然，很难快速get到其中的知识核心与原理。
泰勒级数的产生
要想理解泰勒级数，就得先跳脱出泰勒级数本身的表达式。我们可以思考这样一个问题：在积分与求导运算中，有诸多种类的基本初等函数。那在这些函数中，哪一个只要一出现基本上就能快速求导，求积分？ 非幂函数（power function）莫属。那问题又来了，如果有一个公式可以使所有的函数都能够变成幂函数，这岂不是很快乐？泰勒就是这项快乐的发明者，他说 “在我眼里，所有的函数都是幂函数”。
这句话一出便轰动了微积分界，大家都在思考泰勒如何可以做到这一步？泰勒级数便由此产生。这个公式的伟大之处在于它适用于所有的函数，在尚且不知道f(x)的具体表达式的前提下，它依然可以正常书写出一个通用的公式。
等式的右边虽然看上去很复杂，但是f(a)，f'(a)等都是已知数，只有一个未知数x。虽然f(x)不知是哪个函数，但其对应的多项式已经产生了，右边的每一项分别代表着常数项、x的一次项、x的二次项。
泰勒果真把一个函数写成了这样一个多项式函数的形式，函数的求导与求积分运算将更加简单。但是要充分理解这个表达式，仅仅知道它实现了什么目标远远不够，我们还要知道它为什么这么写？
泰勒级数公式的探究
我们可以先看公式的前半段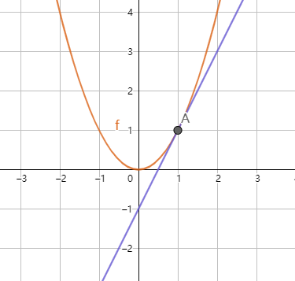
有没有越看越眼熟？没错，这是线性近似（linear approximation）的公式，线性近似指的是当无法得到函数的表达式的情况下，可以通过已知点推导未知点，具体如下所示：
在计算f(2)时，在原函数的表达式未知的前提下，我们可以利用f(x)在(1, 1)点处的信息计算，记作f(2)=f(1)+f’(1)(2-1)，这和泰勒级数的前半段表达式是完全一致的。同时我们也知道这个线性近似并不是十分准确，和实际值差出了1。这是为什么？是因为直线和曲线的增长性不一样吗？
事实上，二者都是单调递增的，之所以产生误差的原因是曲线在这个过程存在着凹凸变化，而直线并没有凹凸性，因此直线与曲线存在着偏差。那如何能够将这个凹凸性的原因考虑在内呢？我们只需要在近似的过程中引入凹凸性的修正，于是泰勒公式的下一项便出现了。
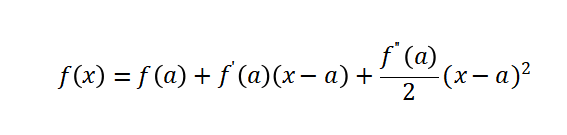带着二阶导的这一项，正是对凹凸性的修正。但凹凸性修正完并不是结束，这并不能保证后面就可以与函数契合到一起，因此还需要更高阶的修正，这便产生了泰勒级数的无限延伸，只有写到∞处，它才和函数完全相等。
不过，在我们的考试中，通常并不需要延伸到这么多，延伸到三四项即可。因此理解泰勒级数也不要从整体公式出发，最重要的是了解它能将所有函数都变成多项式函数从而方便运算与求解的作用。另外它是近似求值的一种形式，来源于线性近似并高于线性近似。
虽然泰勒级数在AP考试中是最难知识担当，但当我们了解了它的缘由与作用之后，是不是就会发现简单了很多？只要大家好好理解，充分练习，就会发现它只不过是个纸老虎，搞定微积分全部内容也是指日可待。
文章作者
福利+领取方式
最后TD君为大家送福利！为了帮助同学们更高效地备考2021年AP考试，我们为大家准备了2021年微积分大纲选择样题解析，免费送给大家！欢迎大家扫一扫下方二维码添加小马甲微信，回复「样题4」免费获取，还能进入备考交流群与大家一起备考~已经添加TD客服马甲微信的同学直接领取即可 无需重复添加微信
