在
极限(Limit)的运算过程中,经常会碰到类似的极限?
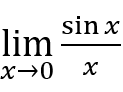
这是
极限部分第一个重要的内容,其计算结果应等于1。但是没有学过的同学肯定会忍不住去想,为什么分母可以为零?在传统数学中,分母难道不是不能为零吗???
无穷小思想的产生
在最初的数学发展中,对于x这个变量定义为
无穷小量,对于无穷小量的认识可以追溯到很久之前。远在春秋战国时期,道家学派代表人物庄子曾举过这样一个例子,“一尺之槌,日取其半,万世不竭”,含义为一根一尺长的木槌,每天砍掉一半,永远都砍不完。木槌的长度就是一个无穷小量。它不等于零,但又与零的意义十分接近。

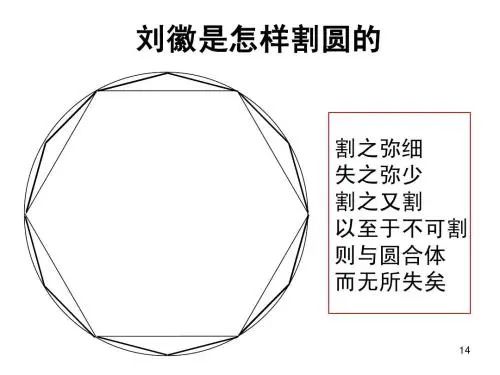
而到了魏晋时期,数学家刘徽在割圆术中也提出过“割之弥细,所失弥少。割之又割,以至于不可割,则与圆合体而无所失矣”的思想,表达出了只要反复进行割圆,那误差就会越来越小,最终和实际的圆并没有什么差别。
微积分
Unit 10的泰勒公式(Taylor series),
拉格朗日误差(Language error bound)以及交替级数误差(Alternating series error bound )也与这一思想有所联系。
微积分的无穷小危机
虽然在微积分的学习过程中,极限的内容在
求导和积分之前,但是微积分在创立初期,牛顿和莱布尼兹这两位大佬都心照不宣的没有解决无穷小量究竟是什么的问题。牛顿在他的物理学研究中,他认为这个x变量是由点、线和面连续运动产生的,所以
他把这个变量称之为“流量”,并把变化率叫做“流数”。
而
莱布尼兹用“瞬”(moment)表示无穷小量,后来也使用了“基元”或“不可分量”进行表示。他曾说过:“对于数学家,为了他们的证明严格起见,只要不要取’无穷小’而取‘要多么小有多么小‘就够了”。可见两位大佬也对这个无穷小量的定义十分头疼。

即便如此,也并不耽误大家使用微积分的热情,
许多数学家都利用微积分来解决实际问题,类似微积分学习中的导数应用与积分应用,即便没有搞清楚极限的概念、无穷小量的概念,但用来解决实际应用问题丝毫没有影响。
正如达朗贝尔所说,现在是“把房子盖的更高些,而不是把基础打得更加牢固”。对于x定义的缺失,使得微积分一直不能成为完整的理论。
到18世纪末,第二次数学危机爆发,数学家发现这种模糊的数学认识,阻碍了微积分的进一步的发展, 其中最著名的是
贝克莱悖论。

贝克莱说,这是“依靠双重错误得到了不科学但却正确的结果”。因为无穷小量在最初的微积分理论中一会说是0,一会说不是0。它对无穷小这一模糊不清的概念进行强烈的抨击:“这些消逝的量说什么呢?它们既不是有限,也不是无限小,又不是零,难道我们不能称它们为消逝量的鬼魂吗?”
极限思想的产生
这一切的解决,依赖于
极限思想的出现,极限思想更像是一种辩证思维,这个无穷小量,“既有零的特性,但又不等于零”。所谓零的特性,是指在某些极限运算中,例如:图片,x可以当作零一样舍弃而不影响结果的可靠性。但它终究是一个无穷小量,可以出现在分母上,并不直接等于零,而是以零为极限。
更加通俗的来说,
本质上x并不是零,但是在特定的场合下,可以当作零被使用,这才是极限的思想。
 极限思想的建立,才使得微积分成为一门完整的学科
极限思想的建立,才使得微积分成为一门完整的学科,虽然它在微积分学习的第一章节,但正是有了这样的基础,在研究其他知识的时候才不会陷入逻辑的矛盾之中,这也是以后学习高等数学过程中需要反复探讨和理解的思想基础。
文章作者

TD福利&领取方式
最后TD君为大家送福利!为帮助大家掌握AP微积分考试中极限的考点,我们整理了该部分所有考试涉及的
极限计算方法以及求导法则。欢迎大家扫一扫下方二维码添加小马甲微信,回复关键词
「极限笔记」即可获取~

推荐阅读
?
AP微积分考前一个月该如何备考?这份备考Tips帮你考前冲刺拿5分
?
0基础考前24小时冲刺AP微观经济5分,我是怎么做到的?-AP微积分5分备考攻略
?
级数收敛的判断方法是什么?熟记7大判别方法,快速进行级数判敛| AP微积分专题级数部分
?
3分钟掌握AP微积分泰勒级数知识点:泰勒级数的产生和公式的探究
?
AP宏/微观经济如何备考拿5分?看完这60张图轻松搞定!-《AP经济图像集》备考资料免费下载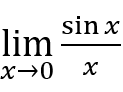 这是极限部分第一个重要的内容,其计算结果应等于1。但是没有学过的同学肯定会忍不住去想,为什么分母可以为零?在传统数学中,分母难道不是不能为零吗???
这是极限部分第一个重要的内容,其计算结果应等于1。但是没有学过的同学肯定会忍不住去想,为什么分母可以为零?在传统数学中,分母难道不是不能为零吗???
 而到了魏晋时期,数学家刘徽在割圆术中也提出过“割之弥细,所失弥少。割之又割,以至于不可割,则与圆合体而无所失矣”的思想,表达出了只要反复进行割圆,那误差就会越来越小,最终和实际的圆并没有什么差别。
微积分Unit 10的泰勒公式(Taylor series),拉格朗日误差(Language error bound)以及交替级数误差(Alternating series error bound )也与这一思想有所联系。
而到了魏晋时期,数学家刘徽在割圆术中也提出过“割之弥细,所失弥少。割之又割,以至于不可割,则与圆合体而无所失矣”的思想,表达出了只要反复进行割圆,那误差就会越来越小,最终和实际的圆并没有什么差别。
微积分Unit 10的泰勒公式(Taylor series),拉格朗日误差(Language error bound)以及交替级数误差(Alternating series error bound )也与这一思想有所联系。

 即便如此,也并不耽误大家使用微积分的热情,许多数学家都利用微积分来解决实际问题,类似微积分学习中的导数应用与积分应用,即便没有搞清楚极限的概念、无穷小量的概念,但用来解决实际应用问题丝毫没有影响。
正如达朗贝尔所说,现在是“把房子盖的更高些,而不是把基础打得更加牢固”。对于x定义的缺失,使得微积分一直不能成为完整的理论。
到18世纪末,第二次数学危机爆发,数学家发现这种模糊的数学认识,阻碍了微积分的进一步的发展, 其中最著名的是贝克莱悖论。
即便如此,也并不耽误大家使用微积分的热情,许多数学家都利用微积分来解决实际问题,类似微积分学习中的导数应用与积分应用,即便没有搞清楚极限的概念、无穷小量的概念,但用来解决实际应用问题丝毫没有影响。
正如达朗贝尔所说,现在是“把房子盖的更高些,而不是把基础打得更加牢固”。对于x定义的缺失,使得微积分一直不能成为完整的理论。
到18世纪末,第二次数学危机爆发,数学家发现这种模糊的数学认识,阻碍了微积分的进一步的发展, 其中最著名的是贝克莱悖论。
 贝克莱说,这是“依靠双重错误得到了不科学但却正确的结果”。因为无穷小量在最初的微积分理论中一会说是0,一会说不是0。它对无穷小这一模糊不清的概念进行强烈的抨击:“这些消逝的量说什么呢?它们既不是有限,也不是无限小,又不是零,难道我们不能称它们为消逝量的鬼魂吗?”
贝克莱说,这是“依靠双重错误得到了不科学但却正确的结果”。因为无穷小量在最初的微积分理论中一会说是0,一会说不是0。它对无穷小这一模糊不清的概念进行强烈的抨击:“这些消逝的量说什么呢?它们既不是有限,也不是无限小,又不是零,难道我们不能称它们为消逝量的鬼魂吗?”
 极限思想的建立,才使得微积分成为一门完整的学科,虽然它在微积分学习的第一章节,但正是有了这样的基础,在研究其他知识的时候才不会陷入逻辑的矛盾之中,这也是以后学习高等数学过程中需要反复探讨和理解的思想基础。
极限思想的建立,才使得微积分成为一门完整的学科,虽然它在微积分学习的第一章节,但正是有了这样的基础,在研究其他知识的时候才不会陷入逻辑的矛盾之中,这也是以后学习高等数学过程中需要反复探讨和理解的思想基础。











