2021年的AP物理C力学第一场考试已经结束,今天官方放出了两个Set的FRQ,我们赶紧一起来看看都考了哪些内容吧!
2021年的AP物理C力学试卷整体难度和知识点
两个Set的对应题目考的知识点相近,第1题主要在考牛顿第二定律和实验分析,Set 1 Q2和Set 2 Q3主要考机械能守恒、弹簧和竖直圆周运动脱离轨道问题,Set 1 Q3和Set 2 Q2主要考连续物体质心位置、积分计算转动惯量、转动的牛顿第二定律和转动动能。此外Set 2 Q3还考了一点平抛运动。
整体的难度中等偏上,涉及实验分析和图像解释的题目可能略难,刚体转动的题目个别小题可能略难。
与往年题目对比的点评
2020年题型特殊不做讨论,
若和2018-2019两年的FRQ相比考点区别还是比较大。
2019年FRQ考察了碰撞中的动量守恒和转动中的角动量守恒,2018年的FRQ也有冲量的计算和角动量定理的应用,而
今年FRQ冲量动量和角动量都没考,应该都放在MCQ里了。
2018年还考察了无滑滚动,今年也没有考。但
今年考察实验误差分析、实验条件改变对实验结果的影响、实验的图像解释比往年多,这种考法不难但要求同学对实验原理和公式有清晰的理解。
另外在刚体转动中质心位置计算、转动惯量对不熟悉微积分的同学可能有些挑战,然后就是在
转动中力矩、角加速度、角速率的变化规律考得比较新颖,很多同学可能知道力矩和角加速度在变小,角速率在变大,但是对于曲线的凹凸性可能不知道如何判断。
再就是
Set 2 Q2里二维刚体的质心高度变化容易算错,有些同学可能会想当然。
2021年的AP物理C力学逐题点评
Set 1
1.一个装有风扇的小车在风扇恒定助推力作用下从一个无摩擦水平面向右滑,3s后滑下一个倾角为θ的斜面,风扇施加的力大小不变。给出了两个运动传感器测出的小车在平面和斜面上加速度随时间变化的图像。

(a) 画出小车在平面和斜面上的受力分析图。
考点:
Unit 2 牛顿运动定律中的受力分析图。
思路:在平面上受到向下的重力、向上的支持力和向右的风扇推力,在斜面上受到向下的重力、垂直斜面向上的支持力和沿斜面向下的风扇推力。
(b) 计算在平面上小车受到的合力。
考点:
Unit 2中的牛顿第二定律。
思路:从图像可得平面上的加速度为 a₁=0.8m/s²,结合牛顿第二定律 F=ma 可得合力。
(c) 计算斜面的倾角θ。
考点:
Unit 2 中的牛顿第二定律。
思路:首先注意传感器的正方向是远离传感器的方向,所以图中 a₂=-2.4m/s² 表示加速度的方向是沿斜面向下。对沿斜面方向列牛顿第二定律方程,重力的分力(大小为mgsinθ)加风扇推力等于质量乘加速度,由此可解得倾角θ。
(d) 如果倾角的实际值比上面(c)中的计算值偏大了3°,考虑下述原因“小车质量没有测准导致倾角没有算准”是否合理?解释你的答案。
考点:
对牛顿第二定律方程的理解 ,实验误差分析。
思路:结合(b)(c)两问列的方程 F=ma₁,mgsinθ+F=m|a₂|,可以发现质量能消掉,得到gsinθ+a₁=|a₂|,所以θ的计算实际上与质量无关。
(e) 对于不同的倾角测出对应的斜面上加速度,给出了 a-sinθ 的图像,要求画出最优拟合线并计算重力加速度g。
考点:
最优拟合线的画法和通过直线斜率计算目标变量。
思路:根据公式 a=gsinθ+a₁,最优拟合线应该是一条直线,注意画的时候不是连接所有点画折线而是要让不在直线上的数据大致平均分布在直线两侧,比如五个数据点可能有两个在直线上、一个在直线上方、两个在直线下方。这条直线的斜率就是g,而计算斜率的时候也要注意不是取数据点而是取直线上的点。
(f) 如果小车的质量变大,但风扇的推力不变,解释(e)中的图像会怎么变。
考点:
还是牛顿第二定律。
思路:根据牛顿第二定律,力不变质量变大,水平面上的加速度a₁会变小,但(e)中的直线方程不变,所以应该是与原直线平行但纵截距变小的一条直线,或者说平行下移了。
2.物块从斜面下滑,经过一个竖直圆轨道,到水平面上压缩一个弹簧。

(a) 画出物块在圆轨道最右端B点的受力分析图。
考点:
Unit 2中的受力分析图。
思路:物块受到向下的重力和水平向左指向圆心的支持力。注意不要再画一个向心力,向心力不是真实的力,只是向心方向合力的效果。
(b) i. 推导B点的速率。
考点:
Unit 3中的机械能守恒。
思路:起点A点的重力势能等于B点的重力势能加动能。
ii. 计算B点的合力
考点:
Unit 2中的圆周运动向心力公式,力的合成。
思路:支持力提供向心力,根据公式可由质量、速率、半径求支持力大小。合力是支持力和重力的矢量和,可用勾股定理求出大小。
(c) 要使物块能通过圆轨道最高点C点而不脱轨,推导所需要的最小释放高度。
考点:
Unit 2中的圆周运动向心力,Unit 3中的机械能守恒。
思路:要使物块能通过圆轨道最高点C点而不脱轨,物块需要有一个最小速率,对应支持力恰好为0、全由重力提供向心力的临界情况,由此解得最小速率。再根据机械能守恒,起点A点的重力势能等于C点的重力势能加动能,解出A点的最小高度。
(d) 给定释放高度和半径的数值(题干中弹簧劲度系数与半径有关),求弹簧的最大压缩量。
考点:
Unit 3中的机械能守恒。
思路:根据机械能守恒,A点的重力势能等于弹簧压缩最大时的弹性势能(这两个状态速率都为0没有动能),列式求解即可。
(e) 给出了弹簧最大压缩量和释放高度之间的关系图像。
i.解释为什么图像第一段 h 小于(c)中计算的最小高度hmin时是一条与横轴重合的水平线。
考点:
Unit 2中的圆周运动向心力,Unit 3中的机械能守恒。
思路:根据机械能守恒,释放高度变小,在圆轨道上各点速率都变小,所需的向心力也就变小,物块还未到达最高点就会出现支持力为0从而脱离轨道的情况,所以无法完成圆周运动,就不会压缩弹簧。
ii.解释图像第二段为什么是这样的形状(上凸函数)。
考点:
Unit 3中的机械能守恒。
思路:根据(d)中机械能守恒的表达式:mgh=½kx²,可得 x∝√h,所以是一个上凸函数。
3.一个细杆有不均匀的线密度,给定总长度L、总质量M和线密度函数λ=γx²。

(a) 用积分证明细杆绕左端点旋转的转动惯量。
考点:
Unit 5中连续物体的转动惯量计算。
思路:在x处取一小段长度为dx的质量微元 dm=λdx=γx²dx,转动惯量为微元转动惯量的积分I=∫x²dm=

代入题目条件即可证明。
(b) 确定细杆质心位置。
考点:
Unit 4中连续物体的质心位置。
思路:还是用微元法,根据连续物体质心位置公式

可解得。
(c) 比较绕端点的转动惯量和绕质心的转动惯量。
考点:
Unit 5中的平行轴定理。
思路:根据平行轴定理,绕平行轴的转动惯量

,绕质心的转动惯量是最小的,所以绕端点的转动惯量大于绕质心的转动惯量。
(d) 细杆从水平位置释放,画出从释放到质心到达最低点过程中,力矩和角速率随时间变化的函数。
考点:
Unit 5中力矩的计算,转动形式的牛顿第二定律,角速率和角加速度的关系。
思路:合力矩就是重力的力矩

,其中θ是转过的角度,而θ随时间增大,所以力矩应该随时间减小,而

,所以斜率的绝对值正比于sinθω随时间增大,所以应该画一个递减的上凸函数。虽然角速率ω在增大,但根据转动牛顿第二定律

,角加速度也在逐渐减小到0,所以ω应该是一个递增的上凸函数,在质心到达最低点时斜率应为0。
(e) 判断角加速度大小是在增大、减小还是不变,说明理由。
考点:Unit 5中力矩的计算,转动形式的牛顿第二定律
思路:同(d)的思路,力矩在逐渐减小,根据转动牛顿第二定律图片,角加速度也在减小。
(f) 求细杆到达竖直位置时底端的线速率。
考点:Unit 3中的机械能守恒,Unit 5中转动动能、角速率和线速率的关系。
思路:根据机械能守恒,最高点的重力势能

等于最低点的转动动能

,由此可以求得最低点角速率;再根据可得速率ν=ωL。注意质心位置不在中点,质心的高度变化不是L/2而是Xc。
Set 2
1.一个探究摩擦力的实验中,物块1放在水平面上,经绕滑轮的绳子连接到悬挂的物块2。知道两个物块的初始质量,质量可调。

(a) 计算能使两个物块保持静止的最小静摩擦系数。
考点:
Unit 2 受力平衡和静摩擦力。
思路:最小静摩擦系数对应物块1将要被向右拉动的临界状态,此时物块1受到向左的最大静摩擦力,对物块1列竖直和水平两个方向的受力平衡方程、对物块2列竖直受力平衡方程,联立求解可得。
(b) 两个物块从静止释放后一起加速度运动,用运动传感器测出了两个物块的加速度。画出两个物块的受力分析图。
考点:
Unit 2受力分析图。
思路:物块1受到向下的重力、向上的支持力、向右的拉力、向左的摩擦力,物块2受到向下的重力和向上的拉力。
(c) 计算物块1与桌面的滑动摩擦系数。
考点:
Unit 2牛顿第二定律、滑动摩擦力。
思路:对物块1和物块2分别列牛顿第二定律方程,根据图中读出的加速度大小即可求解。也可对物块1和2组成的整体列沿绳方向的方程,这样就不用考虑绳子拉力,物块2的重力减去物块1的摩擦力等于总质量乘共同的加速度。
(d) 若实际的动摩擦系数比测出的值偏大,考虑以下解释是否合理:“桌面不完全水平,角度的偏差导致了动摩擦系数的偏差”。
考点:
Unit 2牛顿第二定律、滑动摩擦力。
思路:如果桌面右边偏低,物块1的重力会有一个沿桌面向右的分量,就会使系统整体的加速度偏大、使计算出的摩擦力和摩擦系数比实际偏小。所以这个解释是合理的。
(e) 实验换到一个无摩擦的桌面上,改变两个物块的质量但维持总质量不变,画出加速度和悬挂的物块2的质量的数据图像。
i.画一条最优拟合线
考点:
Unit 2系统的牛顿第二定律,最优拟合线的画法。
思路:根据系统的牛顿第二定律,
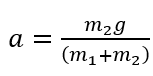
,a和m₂是线性关系,应该画一条直线,让数据点平均分布在直线上下附近。
ii.根据画出的直线计算重力加速度g。
考点:
通过拟合线的斜率计算目标变量。
思路:在线上取两点计算斜率,然后利用
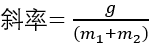
计算g。
(f) 使平面的左端抬起与水平方向成一定角度,问系统的加速度会变大、变小还是不变。
考点:Unit 2系统的牛顿第二定律。
思路:左端抬起后,系统沿运动方向的外力会多一个物块1的重力的分量,外力增大所以加速度也会变大。
2.一个质量均匀的细杆A绕左端点转动。
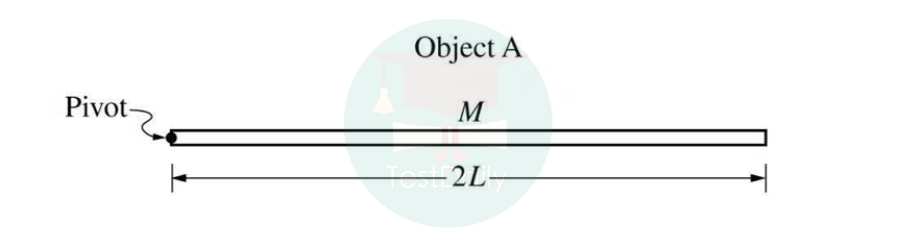
(a) 用积分证明转动惯量。
考点:
Unit 5连续物体的转动惯量。
思路:在距左端x处取一小段长度为dx的质量微元

,转动惯量为微元转动惯量的积分

,即可证明。
(b) 由两根细杆成直角拼接成物体B,求质心的x、y坐标。

考点:
Unit 4 物体的质心位置、质点系的质心位置。
思路:先把两根细杆各自等效为中心出的质点,再利用公式:
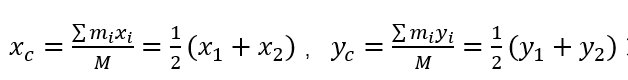
,求解。
(c) 物体B的转动惯量比A大、小还是一样。
考点:
Unit 5转动惯量。
思路:A和B质量相同,但B的右半段比物体A的右半段离转轴更近,根据

,B的转动惯量较小。
(d) 物体B从图中位置释放,画出从释放到质心到达最低点过程中,角加速度和角速率随时间变化的函数。
考点:
Unit 5力矩计算和转动牛顿第二定律,角速率和角加速度的关系。
思路:设转轴到质心的位置矢量为rc,与竖直方向的夹角为φ,则重力的力矩为

,其中φ随时间逐渐减小到0,力矩也随时间逐渐减小到0;为了判断是上凸还是下凸函数,分析
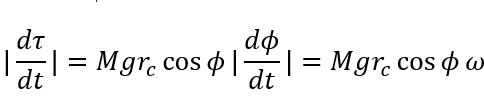
是个增函数,即斜率绝对值在增大,所以

应该是上凸函数,再根据转动牛顿第二定律

,角加速度也是一个递减到0的上凸函数。所以角速度是个递增的下凸函数。
(e) 物体B转过角度θ时,角加速度是在增大、减小还是不变,给出理由。
考点:
Unit 5力矩计算和转动牛顿第二定律。
思路:同(d)中的思路,重力的力矩在减小,根据转动牛顿第二定律,角加速度也在减小。
(f) 求物体B转过90度时的角速率。
考点:
Unit 3机械能守恒和Unit 5转动动能。
思路:根据机械能守恒,减小的重力势能等于增大的转动动能,这里要特别注意的是质心的高度变化怎么计算,应该是在(b)的坐标系中,纵坐标从3/4 L降低到了1/4 L,高度变化是1/2L,而不是物体中点的高度变化L。
3.物块压缩一个竖直弹簧从静止释放,离开弹簧后在空中沿着一个无摩擦圆弧轨道运动然后水平向右离开,做一个平抛运动落回地面。

(a) 画物块在圆轨道最高点的受力分析图。
考点:
Unit 2受力分析图。
思路:物块受向下的重力和向下的支持力。
(b) 求物块在最高点的速率和合力。
考点:
Unit 3机械能守恒和Unit 2圆周运动的向心力。
思路:根据机械能守恒,物块和弹簧一开始具有的弹性势能转化成了物块在最高点的重力势能和动能,知道弹簧压缩量和上升高度就可以把最高点速率求出来。然后在最高点合力提供向心力,根据向心力公式可以求出合力。
(c) 求最小的弹簧压缩量,使得物块可以一直与轨道保持接触到达最高点。
考点:
Unit 2竖直圆周运动脱离轨道的临界条件、Unit 3机械能守恒。
思路:最小弹簧压缩量对应到达最高点具有最小速率,若要一直与轨道接触对应的是到达最高点支持力恰好为0、全由重力提供向心力的情况。根据向心力公式可以算出最小速率,再根据机械能守恒进而算出最小压缩量。
(d) 计算初始压缩量大于最小压缩量时,物块飞出B点做平抛运动的水平距离。
考点:
Unit 3机械能守恒、Unit 1平抛运动。
思路:根据(b)中利用机械能守恒算出的B点水平速率ν,结合平抛运动的知识,算出竖直方向做自由落体运动的时间t,则水平距离D=νt。
(e)题目给出了水平距离D和初始压缩量∆x的函数图像,求解释为什么第一段没有数据,第二段是一条直线且有图中的最小值。
考点:
Unit 3机械能守恒,Unit 2圆周运动,Unit 1平抛运动。
思路:∆x<∆xmin时,根据(c)中的思路,物体无法到达最高点,所以没有数据;∆x≥∆xmin时,根据机械能守恒
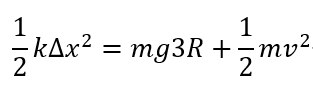
,当重力势能和动能相比很小时,ν和∆x近似成正比,再根据平抛运动公式

,所以D和∆x近似成正比,所以是一条直线,另外根据(c)中分析,最小压缩量∆xmin会对应到达最高点的最小速率νmin,也就对应最小的水平距离Dmin。
文章作者

TD福利
TD整理了CB目前在官网最新更新的
2021年北美卷的AP FRQ真题免费分享给大家,目前共有
AP美国政府与政治、AP物理C电磁、AP物理C力学、AP微积分AB、AP微积分BC、AP德语语言与文化、AP人文地理等7个科目。
有需要的同学可以扫下方二维码,添加TD客服马甲,给马甲发送暗号
「2021frq」即可领取~其他科目真题将随官网更新陆续放入分享链接中,敬请关注~

[series id='363' title='AP真题下载' limit='5']
 (a) 画出小车在平面和斜面上的受力分析图。
考点:Unit 2 牛顿运动定律中的受力分析图。
思路:在平面上受到向下的重力、向上的支持力和向右的风扇推力,在斜面上受到向下的重力、垂直斜面向上的支持力和沿斜面向下的风扇推力。
(b) 计算在平面上小车受到的合力。
考点:Unit 2中的牛顿第二定律。
思路:从图像可得平面上的加速度为 a₁=0.8m/s²,结合牛顿第二定律 F=ma 可得合力。
(c) 计算斜面的倾角θ。
考点:Unit 2 中的牛顿第二定律。
思路:首先注意传感器的正方向是远离传感器的方向,所以图中 a₂=-2.4m/s² 表示加速度的方向是沿斜面向下。对沿斜面方向列牛顿第二定律方程,重力的分力(大小为mgsinθ)加风扇推力等于质量乘加速度,由此可解得倾角θ。
(d) 如果倾角的实际值比上面(c)中的计算值偏大了3°,考虑下述原因“小车质量没有测准导致倾角没有算准”是否合理?解释你的答案。
考点:对牛顿第二定律方程的理解 ,实验误差分析。
思路:结合(b)(c)两问列的方程 F=ma₁,mgsinθ+F=m|a₂|,可以发现质量能消掉,得到gsinθ+a₁=|a₂|,所以θ的计算实际上与质量无关。
(e) 对于不同的倾角测出对应的斜面上加速度,给出了 a-sinθ 的图像,要求画出最优拟合线并计算重力加速度g。
考点:最优拟合线的画法和通过直线斜率计算目标变量。
思路:根据公式 a=gsinθ+a₁,最优拟合线应该是一条直线,注意画的时候不是连接所有点画折线而是要让不在直线上的数据大致平均分布在直线两侧,比如五个数据点可能有两个在直线上、一个在直线上方、两个在直线下方。这条直线的斜率就是g,而计算斜率的时候也要注意不是取数据点而是取直线上的点。
(f) 如果小车的质量变大,但风扇的推力不变,解释(e)中的图像会怎么变。
考点:还是牛顿第二定律。
思路:根据牛顿第二定律,力不变质量变大,水平面上的加速度a₁会变小,但(e)中的直线方程不变,所以应该是与原直线平行但纵截距变小的一条直线,或者说平行下移了。
2.物块从斜面下滑,经过一个竖直圆轨道,到水平面上压缩一个弹簧。
(a) 画出小车在平面和斜面上的受力分析图。
考点:Unit 2 牛顿运动定律中的受力分析图。
思路:在平面上受到向下的重力、向上的支持力和向右的风扇推力,在斜面上受到向下的重力、垂直斜面向上的支持力和沿斜面向下的风扇推力。
(b) 计算在平面上小车受到的合力。
考点:Unit 2中的牛顿第二定律。
思路:从图像可得平面上的加速度为 a₁=0.8m/s²,结合牛顿第二定律 F=ma 可得合力。
(c) 计算斜面的倾角θ。
考点:Unit 2 中的牛顿第二定律。
思路:首先注意传感器的正方向是远离传感器的方向,所以图中 a₂=-2.4m/s² 表示加速度的方向是沿斜面向下。对沿斜面方向列牛顿第二定律方程,重力的分力(大小为mgsinθ)加风扇推力等于质量乘加速度,由此可解得倾角θ。
(d) 如果倾角的实际值比上面(c)中的计算值偏大了3°,考虑下述原因“小车质量没有测准导致倾角没有算准”是否合理?解释你的答案。
考点:对牛顿第二定律方程的理解 ,实验误差分析。
思路:结合(b)(c)两问列的方程 F=ma₁,mgsinθ+F=m|a₂|,可以发现质量能消掉,得到gsinθ+a₁=|a₂|,所以θ的计算实际上与质量无关。
(e) 对于不同的倾角测出对应的斜面上加速度,给出了 a-sinθ 的图像,要求画出最优拟合线并计算重力加速度g。
考点:最优拟合线的画法和通过直线斜率计算目标变量。
思路:根据公式 a=gsinθ+a₁,最优拟合线应该是一条直线,注意画的时候不是连接所有点画折线而是要让不在直线上的数据大致平均分布在直线两侧,比如五个数据点可能有两个在直线上、一个在直线上方、两个在直线下方。这条直线的斜率就是g,而计算斜率的时候也要注意不是取数据点而是取直线上的点。
(f) 如果小车的质量变大,但风扇的推力不变,解释(e)中的图像会怎么变。
考点:还是牛顿第二定律。
思路:根据牛顿第二定律,力不变质量变大,水平面上的加速度a₁会变小,但(e)中的直线方程不变,所以应该是与原直线平行但纵截距变小的一条直线,或者说平行下移了。
2.物块从斜面下滑,经过一个竖直圆轨道,到水平面上压缩一个弹簧。
 (a) 画出物块在圆轨道最右端B点的受力分析图。
考点:Unit 2中的受力分析图。
思路:物块受到向下的重力和水平向左指向圆心的支持力。注意不要再画一个向心力,向心力不是真实的力,只是向心方向合力的效果。
(b) i. 推导B点的速率。
考点:Unit 3中的机械能守恒。
思路:起点A点的重力势能等于B点的重力势能加动能。
ii. 计算B点的合力
考点:Unit 2中的圆周运动向心力公式,力的合成。
思路:支持力提供向心力,根据公式可由质量、速率、半径求支持力大小。合力是支持力和重力的矢量和,可用勾股定理求出大小。
(c) 要使物块能通过圆轨道最高点C点而不脱轨,推导所需要的最小释放高度。
考点:Unit 2中的圆周运动向心力,Unit 3中的机械能守恒。
思路:要使物块能通过圆轨道最高点C点而不脱轨,物块需要有一个最小速率,对应支持力恰好为0、全由重力提供向心力的临界情况,由此解得最小速率。再根据机械能守恒,起点A点的重力势能等于C点的重力势能加动能,解出A点的最小高度。
(d) 给定释放高度和半径的数值(题干中弹簧劲度系数与半径有关),求弹簧的最大压缩量。
考点:Unit 3中的机械能守恒。
思路:根据机械能守恒,A点的重力势能等于弹簧压缩最大时的弹性势能(这两个状态速率都为0没有动能),列式求解即可。
(e) 给出了弹簧最大压缩量和释放高度之间的关系图像。
i.解释为什么图像第一段 h 小于(c)中计算的最小高度hmin时是一条与横轴重合的水平线。
考点:Unit 2中的圆周运动向心力,Unit 3中的机械能守恒。
思路:根据机械能守恒,释放高度变小,在圆轨道上各点速率都变小,所需的向心力也就变小,物块还未到达最高点就会出现支持力为0从而脱离轨道的情况,所以无法完成圆周运动,就不会压缩弹簧。
ii.解释图像第二段为什么是这样的形状(上凸函数)。
考点:Unit 3中的机械能守恒。
思路:根据(d)中机械能守恒的表达式:mgh=½kx²,可得 x∝√h,所以是一个上凸函数。
3.一个细杆有不均匀的线密度,给定总长度L、总质量M和线密度函数λ=γx²。
(a) 画出物块在圆轨道最右端B点的受力分析图。
考点:Unit 2中的受力分析图。
思路:物块受到向下的重力和水平向左指向圆心的支持力。注意不要再画一个向心力,向心力不是真实的力,只是向心方向合力的效果。
(b) i. 推导B点的速率。
考点:Unit 3中的机械能守恒。
思路:起点A点的重力势能等于B点的重力势能加动能。
ii. 计算B点的合力
考点:Unit 2中的圆周运动向心力公式,力的合成。
思路:支持力提供向心力,根据公式可由质量、速率、半径求支持力大小。合力是支持力和重力的矢量和,可用勾股定理求出大小。
(c) 要使物块能通过圆轨道最高点C点而不脱轨,推导所需要的最小释放高度。
考点:Unit 2中的圆周运动向心力,Unit 3中的机械能守恒。
思路:要使物块能通过圆轨道最高点C点而不脱轨,物块需要有一个最小速率,对应支持力恰好为0、全由重力提供向心力的临界情况,由此解得最小速率。再根据机械能守恒,起点A点的重力势能等于C点的重力势能加动能,解出A点的最小高度。
(d) 给定释放高度和半径的数值(题干中弹簧劲度系数与半径有关),求弹簧的最大压缩量。
考点:Unit 3中的机械能守恒。
思路:根据机械能守恒,A点的重力势能等于弹簧压缩最大时的弹性势能(这两个状态速率都为0没有动能),列式求解即可。
(e) 给出了弹簧最大压缩量和释放高度之间的关系图像。
i.解释为什么图像第一段 h 小于(c)中计算的最小高度hmin时是一条与横轴重合的水平线。
考点:Unit 2中的圆周运动向心力,Unit 3中的机械能守恒。
思路:根据机械能守恒,释放高度变小,在圆轨道上各点速率都变小,所需的向心力也就变小,物块还未到达最高点就会出现支持力为0从而脱离轨道的情况,所以无法完成圆周运动,就不会压缩弹簧。
ii.解释图像第二段为什么是这样的形状(上凸函数)。
考点:Unit 3中的机械能守恒。
思路:根据(d)中机械能守恒的表达式:mgh=½kx²,可得 x∝√h,所以是一个上凸函数。
3.一个细杆有不均匀的线密度,给定总长度L、总质量M和线密度函数λ=γx²。
 (a) 用积分证明细杆绕左端点旋转的转动惯量。
考点:Unit 5中连续物体的转动惯量计算。
思路:在x处取一小段长度为dx的质量微元 dm=λdx=γx²dx,转动惯量为微元转动惯量的积分I=∫x²dm=
(a) 用积分证明细杆绕左端点旋转的转动惯量。
考点:Unit 5中连续物体的转动惯量计算。
思路:在x处取一小段长度为dx的质量微元 dm=λdx=γx²dx,转动惯量为微元转动惯量的积分I=∫x²dm= 可解得。
(c) 比较绕端点的转动惯量和绕质心的转动惯量。
考点:Unit 5中的平行轴定理。
思路:根据平行轴定理,绕平行轴的转动惯量
可解得。
(c) 比较绕端点的转动惯量和绕质心的转动惯量。
考点:Unit 5中的平行轴定理。
思路:根据平行轴定理,绕平行轴的转动惯量 ,绕质心的转动惯量是最小的,所以绕端点的转动惯量大于绕质心的转动惯量。
(d) 细杆从水平位置释放,画出从释放到质心到达最低点过程中,力矩和角速率随时间变化的函数。
考点:Unit 5中力矩的计算,转动形式的牛顿第二定律,角速率和角加速度的关系。
思路:合力矩就是重力的力矩
,绕质心的转动惯量是最小的,所以绕端点的转动惯量大于绕质心的转动惯量。
(d) 细杆从水平位置释放,画出从释放到质心到达最低点过程中,力矩和角速率随时间变化的函数。
考点:Unit 5中力矩的计算,转动形式的牛顿第二定律,角速率和角加速度的关系。
思路:合力矩就是重力的力矩 ,其中θ是转过的角度,而θ随时间增大,所以力矩应该随时间减小,而
,其中θ是转过的角度,而θ随时间增大,所以力矩应该随时间减小,而 ,所以斜率的绝对值正比于sinθω随时间增大,所以应该画一个递减的上凸函数。虽然角速率ω在增大,但根据转动牛顿第二定律
,所以斜率的绝对值正比于sinθω随时间增大,所以应该画一个递减的上凸函数。虽然角速率ω在增大,但根据转动牛顿第二定律 (a) 计算能使两个物块保持静止的最小静摩擦系数。
考点:Unit 2 受力平衡和静摩擦力。
思路:最小静摩擦系数对应物块1将要被向右拉动的临界状态,此时物块1受到向左的最大静摩擦力,对物块1列竖直和水平两个方向的受力平衡方程、对物块2列竖直受力平衡方程,联立求解可得。
(b) 两个物块从静止释放后一起加速度运动,用运动传感器测出了两个物块的加速度。画出两个物块的受力分析图。
考点:Unit 2受力分析图。
思路:物块1受到向下的重力、向上的支持力、向右的拉力、向左的摩擦力,物块2受到向下的重力和向上的拉力。
(c) 计算物块1与桌面的滑动摩擦系数。
考点:Unit 2牛顿第二定律、滑动摩擦力。
思路:对物块1和物块2分别列牛顿第二定律方程,根据图中读出的加速度大小即可求解。也可对物块1和2组成的整体列沿绳方向的方程,这样就不用考虑绳子拉力,物块2的重力减去物块1的摩擦力等于总质量乘共同的加速度。
(d) 若实际的动摩擦系数比测出的值偏大,考虑以下解释是否合理:“桌面不完全水平,角度的偏差导致了动摩擦系数的偏差”。
考点:Unit 2牛顿第二定律、滑动摩擦力。
思路:如果桌面右边偏低,物块1的重力会有一个沿桌面向右的分量,就会使系统整体的加速度偏大、使计算出的摩擦力和摩擦系数比实际偏小。所以这个解释是合理的。
(e) 实验换到一个无摩擦的桌面上,改变两个物块的质量但维持总质量不变,画出加速度和悬挂的物块2的质量的数据图像。
i.画一条最优拟合线
考点:Unit 2系统的牛顿第二定律,最优拟合线的画法。
思路:根据系统的牛顿第二定律,
(a) 计算能使两个物块保持静止的最小静摩擦系数。
考点:Unit 2 受力平衡和静摩擦力。
思路:最小静摩擦系数对应物块1将要被向右拉动的临界状态,此时物块1受到向左的最大静摩擦力,对物块1列竖直和水平两个方向的受力平衡方程、对物块2列竖直受力平衡方程,联立求解可得。
(b) 两个物块从静止释放后一起加速度运动,用运动传感器测出了两个物块的加速度。画出两个物块的受力分析图。
考点:Unit 2受力分析图。
思路:物块1受到向下的重力、向上的支持力、向右的拉力、向左的摩擦力,物块2受到向下的重力和向上的拉力。
(c) 计算物块1与桌面的滑动摩擦系数。
考点:Unit 2牛顿第二定律、滑动摩擦力。
思路:对物块1和物块2分别列牛顿第二定律方程,根据图中读出的加速度大小即可求解。也可对物块1和2组成的整体列沿绳方向的方程,这样就不用考虑绳子拉力,物块2的重力减去物块1的摩擦力等于总质量乘共同的加速度。
(d) 若实际的动摩擦系数比测出的值偏大,考虑以下解释是否合理:“桌面不完全水平,角度的偏差导致了动摩擦系数的偏差”。
考点:Unit 2牛顿第二定律、滑动摩擦力。
思路:如果桌面右边偏低,物块1的重力会有一个沿桌面向右的分量,就会使系统整体的加速度偏大、使计算出的摩擦力和摩擦系数比实际偏小。所以这个解释是合理的。
(e) 实验换到一个无摩擦的桌面上,改变两个物块的质量但维持总质量不变,画出加速度和悬挂的物块2的质量的数据图像。
i.画一条最优拟合线
考点:Unit 2系统的牛顿第二定律,最优拟合线的画法。
思路:根据系统的牛顿第二定律,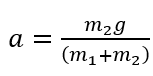 ,a和m₂是线性关系,应该画一条直线,让数据点平均分布在直线上下附近。
ii.根据画出的直线计算重力加速度g。
考点:通过拟合线的斜率计算目标变量。
思路:在线上取两点计算斜率,然后利用
,a和m₂是线性关系,应该画一条直线,让数据点平均分布在直线上下附近。
ii.根据画出的直线计算重力加速度g。
考点:通过拟合线的斜率计算目标变量。
思路:在线上取两点计算斜率,然后利用 (a) 用积分证明转动惯量。
考点:Unit 5连续物体的转动惯量。
思路:在距左端x处取一小段长度为dx的质量微元
(a) 用积分证明转动惯量。
考点:Unit 5连续物体的转动惯量。
思路:在距左端x处取一小段长度为dx的质量微元 ,转动惯量为微元转动惯量的积分
,转动惯量为微元转动惯量的积分 ,即可证明。
(b) 由两根细杆成直角拼接成物体B,求质心的x、y坐标。
,即可证明。
(b) 由两根细杆成直角拼接成物体B,求质心的x、y坐标。
 考点:Unit 4 物体的质心位置、质点系的质心位置。
思路:先把两根细杆各自等效为中心出的质点,再利用公式:
考点:Unit 4 物体的质心位置、质点系的质心位置。
思路:先把两根细杆各自等效为中心出的质点,再利用公式:
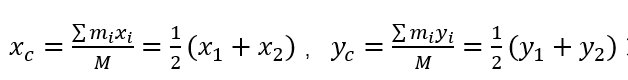 ,求解。
(c) 物体B的转动惯量比A大、小还是一样。
考点:Unit 5转动惯量。
思路:A和B质量相同,但B的右半段比物体A的右半段离转轴更近,根据
,求解。
(c) 物体B的转动惯量比A大、小还是一样。
考点:Unit 5转动惯量。
思路:A和B质量相同,但B的右半段比物体A的右半段离转轴更近,根据 ,B的转动惯量较小。
(d) 物体B从图中位置释放,画出从释放到质心到达最低点过程中,角加速度和角速率随时间变化的函数。
考点:Unit 5力矩计算和转动牛顿第二定律,角速率和角加速度的关系。
思路:设转轴到质心的位置矢量为rc,与竖直方向的夹角为φ,则重力的力矩为
,B的转动惯量较小。
(d) 物体B从图中位置释放,画出从释放到质心到达最低点过程中,角加速度和角速率随时间变化的函数。
考点:Unit 5力矩计算和转动牛顿第二定律,角速率和角加速度的关系。
思路:设转轴到质心的位置矢量为rc,与竖直方向的夹角为φ,则重力的力矩为
 ,其中φ随时间逐渐减小到0,力矩也随时间逐渐减小到0;为了判断是上凸还是下凸函数,分析
,其中φ随时间逐渐减小到0,力矩也随时间逐渐减小到0;为了判断是上凸还是下凸函数,分析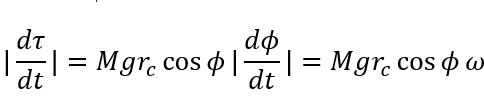 是个增函数,即斜率绝对值在增大,所以
是个增函数,即斜率绝对值在增大,所以 应该是上凸函数,再根据转动牛顿第二定律
应该是上凸函数,再根据转动牛顿第二定律 (a) 画物块在圆轨道最高点的受力分析图。
考点:Unit 2受力分析图。
思路:物块受向下的重力和向下的支持力。
(b) 求物块在最高点的速率和合力。
考点:Unit 3机械能守恒和Unit 2圆周运动的向心力。
思路:根据机械能守恒,物块和弹簧一开始具有的弹性势能转化成了物块在最高点的重力势能和动能,知道弹簧压缩量和上升高度就可以把最高点速率求出来。然后在最高点合力提供向心力,根据向心力公式可以求出合力。
(c) 求最小的弹簧压缩量,使得物块可以一直与轨道保持接触到达最高点。
考点:Unit 2竖直圆周运动脱离轨道的临界条件、Unit 3机械能守恒。
思路:最小弹簧压缩量对应到达最高点具有最小速率,若要一直与轨道接触对应的是到达最高点支持力恰好为0、全由重力提供向心力的情况。根据向心力公式可以算出最小速率,再根据机械能守恒进而算出最小压缩量。
(d) 计算初始压缩量大于最小压缩量时,物块飞出B点做平抛运动的水平距离。
考点:Unit 3机械能守恒、Unit 1平抛运动。
思路:根据(b)中利用机械能守恒算出的B点水平速率ν,结合平抛运动的知识,算出竖直方向做自由落体运动的时间t,则水平距离D=νt。
(e)题目给出了水平距离D和初始压缩量∆x的函数图像,求解释为什么第一段没有数据,第二段是一条直线且有图中的最小值。
考点:Unit 3机械能守恒,Unit 2圆周运动,Unit 1平抛运动。
思路:∆x<∆xmin时,根据(c)中的思路,物体无法到达最高点,所以没有数据;∆x≥∆xmin时,根据机械能守恒
(a) 画物块在圆轨道最高点的受力分析图。
考点:Unit 2受力分析图。
思路:物块受向下的重力和向下的支持力。
(b) 求物块在最高点的速率和合力。
考点:Unit 3机械能守恒和Unit 2圆周运动的向心力。
思路:根据机械能守恒,物块和弹簧一开始具有的弹性势能转化成了物块在最高点的重力势能和动能,知道弹簧压缩量和上升高度就可以把最高点速率求出来。然后在最高点合力提供向心力,根据向心力公式可以求出合力。
(c) 求最小的弹簧压缩量,使得物块可以一直与轨道保持接触到达最高点。
考点:Unit 2竖直圆周运动脱离轨道的临界条件、Unit 3机械能守恒。
思路:最小弹簧压缩量对应到达最高点具有最小速率,若要一直与轨道接触对应的是到达最高点支持力恰好为0、全由重力提供向心力的情况。根据向心力公式可以算出最小速率,再根据机械能守恒进而算出最小压缩量。
(d) 计算初始压缩量大于最小压缩量时,物块飞出B点做平抛运动的水平距离。
考点:Unit 3机械能守恒、Unit 1平抛运动。
思路:根据(b)中利用机械能守恒算出的B点水平速率ν,结合平抛运动的知识,算出竖直方向做自由落体运动的时间t,则水平距离D=νt。
(e)题目给出了水平距离D和初始压缩量∆x的函数图像,求解释为什么第一段没有数据,第二段是一条直线且有图中的最小值。
考点:Unit 3机械能守恒,Unit 2圆周运动,Unit 1平抛运动。
思路:∆x<∆xmin时,根据(c)中的思路,物体无法到达最高点,所以没有数据;∆x≥∆xmin时,根据机械能守恒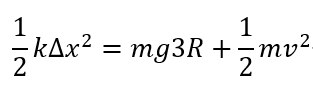 ,当重力势能和动能相比很小时,ν和∆x近似成正比,再根据平抛运动公式
,当重力势能和动能相比很小时,ν和∆x近似成正比,再根据平抛运动公式 ,所以D和∆x近似成正比,所以是一条直线,另外根据(c)中分析,最小压缩量∆xmin会对应到达最高点的最小速率νmin,也就对应最小的水平距离Dmin。
,所以D和∆x近似成正比,所以是一条直线,另外根据(c)中分析,最小压缩量∆xmin会对应到达最高点的最小速率νmin,也就对应最小的水平距离Dmin。

 [series id='363' title='AP真题下载' limit='5']
[series id='363' title='AP真题下载' limit='5']










