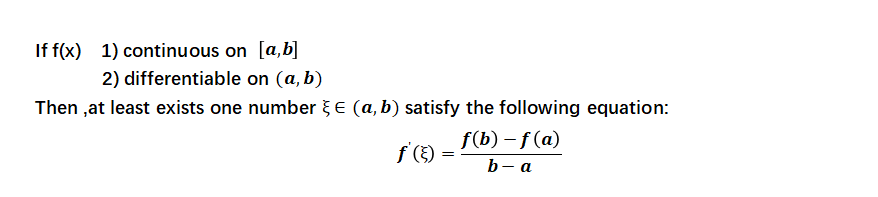在AP微积分的考试里,导数应用中存在着一个定理,“背景庞大”,同时也是高频考点,称之为
中值定理(Mean Value Theorem)。在AP微积分考试中,中值定理特指的是拉格朗日中值定理,但在书本上对其原理的描述总是寥寥无几。
这主要是缺少了一个先决条件—拉格朗日中定理是建立在罗尔定理的认识基础上的,利用罗尔定理才能真正理解它的来源。
罗尔原本并不是微积分舞台上的数学家,甚至他是早期微积分学的批评家。当年牛顿在到处宣传自己的微积分运算,但是罗尔却认为微积分是建立在不稳固的理论上的,这个在之前的推文中曾经提到,因为无穷小的不确定,引发了数学危机 ?:
AP微积分之极限的概念:让牛顿和莱布尼兹都头疼的极限问题到底是什么?
但是没有人能够脱离“真香定律”,罗尔在对微积分的抵制之中,最终慢慢的被这个学科所吸引,最后大笔一挥,
写出了罗尔定理(Rolle’s Theorem)。
[caption id="" align="aligncenter" width="226"]

罗尔中值定理(Rolle’s Theorem)[/caption]
罗尔定理描述如下:
证明:因为函数 f(x) 在闭区间[a,b] 上连续,所以存在最大值与最小值,分别用 M 和 m 表示,分两种情况讨论:
1. 若 M=m,则函数 f(x) 在闭区间 [a,b] 上必为常函数,结论显然成立。
2. 若 M>m,则因为 f(a)=f(b) 使得最大值 M 与最小值 m 至少有一个在 (a,b) 内某点ξ处取得,从而ξ是f(x)的极值点,又条件 f(x) 在开区间 (a,b) 内可导得,f(x) 在 ξ 处取得极值,可导的极值点一定是驻点,推知:f'(ξ)=0。
对于罗尔定理的理解,更好的办法是借助于几何图像,如果满足以上三个基本条件,图像的表现形式则为下图形式,此时一定会有一点的处的切线为水平线,即导数等于零。
[caption id="" align="aligncenter" width="297"]

拉格朗日中值定理(Mean Value Theorem)[/caption]
相较于罗尔,拉格朗日就是微积分学的名人了,很多同学在AP微积分BC考试中的噩梦-
拉格朗日误差(Lagrange Error Bound),也是它发明的。但实际上拉格朗日在数学、力学和天文学三个学科中都有重大历史性贡献,但他主要是数学家,研究力学和天文学的目的是表明数学分析的威力。全部著作、论文、学术报告记录、学术通讯超过500篇。并且据说它和披靡一时的拿破仑也是好朋友。在后面的文章中我们会对它展开专门的介绍。
拉格朗日中值定理(Mean Value Theorem)又称拉氏定理,是微分学中的基本定理之一,它反映了可导函数在闭区间上的整体的平均变化率与区间内某点的局部变化率的关系。拉格朗日中值定理是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形,是泰勒公式的弱形式(一阶展开)。其描述如下:
如何利用罗尔定理证明拉格朗日定理呢?这里需要借助构建辅助函数的方式,构建出恰好相等的两个数值,证明如下:
同时也可以利用几何构型进行理解,连接AB两点后,发现AB连线的割线斜率与C₁与C₂点的斜率相同,因此有f’(C₁)=
在AP考试中,并不涉及对于罗尔定理的考察,但是会对拉格朗日中定理进行考察,而考察的方式,主要是考察书写定理以及根据题目含义,去挖掘这个定理。
文章作者
TD福利&领取方式
在2021年的A3线上考试中,对于定理性质的知识情有独钟,进行了大量的考察。非常考验大家对于定理本身以及其含义的理解。特此为大家附赠了一份历年真题中对中值定理考察的练习题,帮助大家学习巩固中值定理的题目。
有需要的同学可以扫下方二维码,添加TD客服马甲,给马甲发送暗号
「中值定理」即可领取~

推荐阅读
?
牛顿、莱布尼兹到底谁是“微积分之父”?微积分经典之战了解一下
?
美国大学微积分课程如何自学?这5门网课和6本教材推荐给你!
?
2021年AP微积分AB北美卷FRQ真题下载:高频考点与往年相似,但有难题
?
AP微积分定理考察题型:极限定理/介质定理/中值定理/均值定理知识点总结
?
AP 19科近10年FRQ真题合集,免费下载领取-AP微积分、物理等19门真题免费下载
- AP考试研习社 微信号:gh_db4a8475809b
- TD旗下专注于AP/A Level/IB/AMC等理科项目的原创资料研发、教学教研分享、教学产品设计的公众号,为中国留学生提供和国际化接轨的理科教学服务.
- *侵权请邮件联系563067852@qq.com,安排删除。
 罗尔中值定理(Rolle’s Theorem)[/caption]
罗尔中值定理(Rolle’s Theorem)[/caption]
 罗尔中值定理(Rolle’s Theorem)[/caption]
罗尔中值定理(Rolle’s Theorem)[/caption]
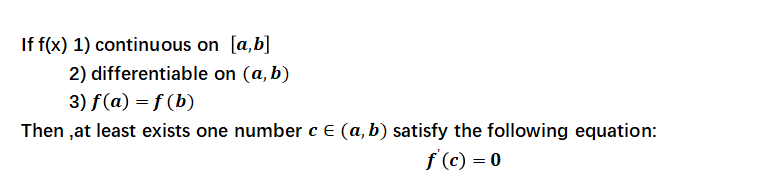
 拉格朗日中值定理(Mean Value Theorem)[/caption]
拉格朗日中值定理(Mean Value Theorem)[/caption]
 拉格朗日中值定理(Mean Value Theorem)[/caption]
拉格朗日中值定理(Mean Value Theorem)[/caption]