在实数域中，连接两个真理的最短的路径是通过复数域。——雅克·阿达马 无论在何种教育体系下，欧洲体系，北美体系又或者是国内体系下，学习复数的标准方式都是利用叫做 x²+4=0 的方程。在传统的实数系中，解决一个类似的二次方程通常对两边取根号，然后对结果进行讨论。但是这种方法只适用于存在着实数根的例子，一旦变成 x²+4=0 这样的情况，就变得毫无办法。因为在实数范围内，并没有任何一个数的平方等于-4。

负根号的产生

其实对于这一问题，从文艺复兴时期，数学家卡尔达诺就对此展开了讨论，他讨论找到和为10且乘积为40的两个数的问题，即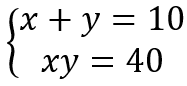
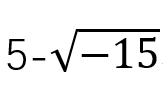
利用二次函数的公式法，可以得到结果为
和
这仿佛就像是本来就没有意义的事情，因为不存在为何还要进行研究？就如同前面的
既不等于2，也不等于-2，只是一个表达形式，而并不具备数字本身的意义。
其实这种想法十分合理，这就如同去求解这两个方程的公共解，我们可以将它的图像描绘出来，解不出来就意味着没有解，既然没有解，就不需要继续探讨了。
[caption id="" align="aligncenter" width="514"] x+y=10 & xy=40的图像[/caption]

图像与代数的矛盾

于是卡尔达诺又“开心地”做起了其他内容的探讨，经过长时间的数学研究，他找到了求解三次方程的公式，通俗地讲：
这是卡尔达诺一生最伟大的公式，但是命运的安排总是充满戏剧性，这个公式虽然是准确的，但是不可避免地又出现了复数的身影。假设方程为 x³-15x-4=0，利用上面的公式
按照实数领域的认识，这个数字应该是不存在。但是当把图像绘制出来（如下图），会发现其实它的根是存在的。
[caption id="" align="aligncenter" width="476"] y=x³-15x-4的图像[/caption]

虚数的诞生

直到他去世也没有解决这个问题，公式其实是准确的，只不过缺少了一个新的数系作为媒介去连接不同的数值。这个问题最终在笛卡尔等数学家的努力下得到了解决，而此时这一符号也正式问世。 至此，人类开始以 i 定义数字
其运算规则为 i²=-1 同时也给它命名了一个好听的名字虚数（imaginary number），意为想象中的数字。以代表实数（real number）的对立面。而同时，如果将实数与虚数糅合到一起，便称为复数（complex number）。
而卡尔达诺跨越一个世纪的问题也得到了解答。
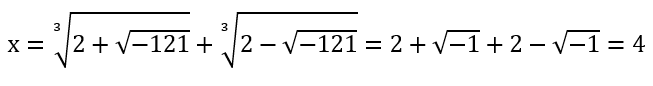
在化简之中 i 相互抵消，至此人们也明白了i 存在的真正意义——作为中间的媒介简化实数运算。 而复数在高中阶段也是重要的考试内容，在SAT考试中，会考察复数的四则运算，将虚数与实数结合在一起，进行形如a+bi型数字的运算。 在美高课程Pre-Calculus中，除了四则运算外，还会考察复数的极坐标与指数表达形式，复数方程求解，以及德莫夫定律。除了a+bi这一种形式以外，还需要认识 r·cisθ，以及这两种形式的复数方程，而极坐标形式还可以帮助解决形如 z²+1=i 这种形式的复数方程。 在IB知识体系中，除了上述知识，还会涉及到欧拉公式以及麦克劳林级数与欧拉公式的证明。即为什么可以用
代替复数的写法，通过
的麦克劳林展开式可以建立二者之间的关系。 因此复数在高中的考试中经常出现，它是理解实数规律的便捷工具，同时也是考试中的送分点，通常不会有太大的难度，但充分理解也是必要的，否则就很难弄清楚自己在进行什么运算。

文章作者

福利赠送

为了方便大家进一步了解SAT、IB和预备微积分中复数考察的具体要求，TD为大家整理了相关内容的大纲文件和教材说明。
1. TestDaily分享-新SAT官方指南, Page 254-255 2. TestDaily分享-Precalculus, 6 Edition, Page 793-811 3. TestDaily分享-Mathematics HL Guide 2014, Page 27-28
有需要的同学可以扫描下方二维码，添加小马甲，回复关键词「复数」，即可领取！

推荐阅读

?AP微积分估值2种方法之：黎曼与梯形法及泰勒级数介绍 ?AP微积分考试必须掌握的2种估值方法，你学会了吗？-AP微积分答题技巧 ?AP微积分备考教材教辅良心推荐！附赠搭配使用说明，可免费下载！ ?AP微积分/宏微观经济学/统计学学习资源网站推荐，用过都说好！ ?AP微积分考试中3个计算器使用小技巧，提高答题速度和正确率全靠它！
  • AP考试研习社    微信号：gh_db4a8475809b
  • TD旗下专注于AP/A Level/IB/AMC等理科项目的原创资料研发、教学教研分享、教学产品设计的公众号,为中国留学生提供和国际化接轨的理科教学服务.
  • *侵权请邮件联系563067852@qq.com，安排删除。