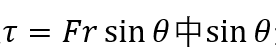
[caption id="" align="aligncenter" width="900"] (2011 Intl MCQ 25-26)[/caption]
(2011 Intl MCQ 25-26)[/caption]
2011年的一道MCQ,如图所示,说有一根细杆从竖直位置开始受到轻微扰动而向下转动,转过的角度为θ。首先让我们求的是角加速度α和角度θ的图像。
根据转动的牛顿第二定律,角加速度等于力矩除以转动惯量,其中转动惯量是定值,而力矩随着转动再逐渐增大;假设转轴到质心的距离为r,则细杆受到顺时针的力矩大小为
 (2011 Intl MCQ 25-26)[/caption]
(2011 Intl MCQ 25-26)[/caption]
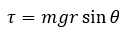
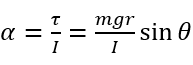
[caption id="" align="aligncenter" width="900"] (2011 Intl MCQ 25)[/caption]
(2011 Intl MCQ 25)[/caption]
第二小问让我们继续求角速度ω随时间t变化的图像。这里一个误区是由同学想着“角速度是角加速度求积分,sin函数求积分是cos函数……”这就走远了。
ω(t)=ʃ α(t)dt 是对时间积分,要得到α(t)才能算积分,可是现在得到的是α关于角度θ的函数,实际上表示了一个二阶非线性微分方程,要求解非常复杂,求出来的ω(t)也不是cos函数的形式,找cos函数的图像也选不对答案。实际上这题不需要得到具体的ω(t)函数。
可以说随着时间增大,转过角度增大,力矩增大,角加速度增大,所以ω-t图像斜率增大,是上凹函数(concave upward,亦即下凸)。也就是说这题其实并没有什么微积分知识,只需要知道角加速度是角速度图像的斜率,会用转动牛顿第二定律分析角加速度就可以了,还是在考物理概念。正确答案如下:
 (2011 Intl MCQ 25)[/caption]
(2011 Intl MCQ 25)[/caption]
[caption id="" align="aligncenter" width="900"]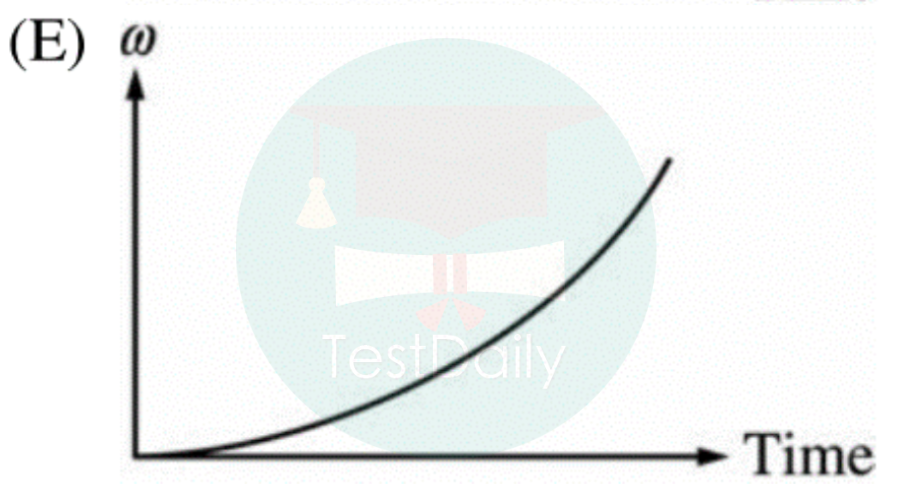 (2011 Intl MCQ 26)[/caption]
(2011 Intl MCQ 26)[/caption]
这两道题都不用真的推导出函数表达式进行求导,就可以说明图像的凹凸性,但有的题目要严格证明凹凸性就略复杂一些。这时候就真正考验大家求导数的基本功了!
如果导数增大,函数图像上凹;如果导数减小,函数图像下凹。这个在FRQ的画图题中是个采分点,只画对了增减性但没画对凹凸性是不得分的。因为评分标准中会说“For a concave down curve that decreases to zero for the graph of ……”。
下面我们就来看这样一道题,2021年最新的FRQ。一个如图所示的细杆绕左端点从水平位置开始顺时针向下转动,让我们画出力矩和时间的函数图像。
 (2011 Intl MCQ 26)[/caption]
(2011 Intl MCQ 26)[/caption]
[caption id="" align="aligncenter" width="900"] (2021 NA Set1 FRQ3)[/caption]
(2021 NA Set1 FRQ3)[/caption]
由于题目条件说这是一个密度不均匀的细杆,所以质心并不在中点,但是这对我们画图没有影响。假设转轴到细杆的质心距离为r,转过的角度为θ,则力矩为
 (2021 NA Set1 FRQ3)[/caption]
(2021 NA Set1 FRQ3)[/caption]




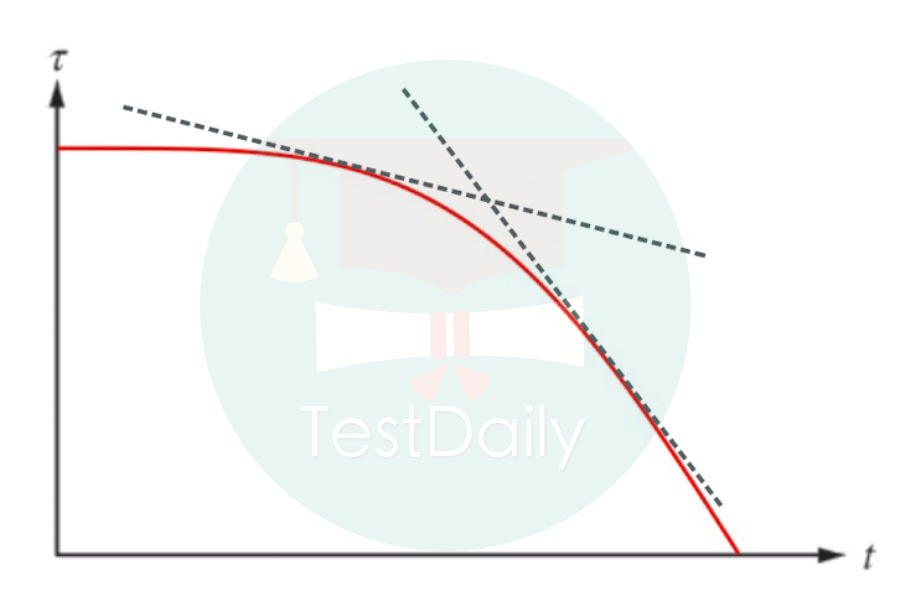
 2. 得不到直接关于横坐标的表达式,例如图3得不到τ(t),但可以通过某些中间变量比如θ计算出一个可以判断变化规律的导数/斜率表达式
2. 得不到直接关于横坐标的表达式,例如图3得不到τ(t),但可以通过某些中间变量比如θ计算出一个可以判断变化规律的导数/斜率表达式
TD福利&领取方式
为了帮助大家更多掌握转动中的函数图像问题在FRQ中的考察,我们特别准备了「AP物理C力学历年FRQ刷题集」送给大家。推文中的例题来自于2021年的Set 1,而在2021 Set 2中考了一道类似的画图题,大家可以拿它检测一下自己学会了吗~ 有需要的同学可以扫描下方二维码,添加TD客服马甲,给马甲发送暗号「凹凸」即可领取~
- AP考试研习社 微信号:gh_db4a8475809b
- *侵权请邮件联系563067852@qq.com,安排删除。










