计数Counting和数论Number Theory是AMC考试中最核心的内容,也是正在紧张备考过程中同学们遇到的最多类型的题目,其中Probability概率问题也是一种最容易玩儿出花样的从属类型题目,相信到了目前阶段的同学们或多或少地都已经积攒了些许做题的心得。很多同学都慢慢发现做AMC题目有点像“坐过山车”。
有时候感觉题目真的很简单,什么排列组合、加法乘法、杨辉三角二项式定理,小学奥数统统都学过,前期题目做得太顺甚至有同学发出感叹:“咦,奇了怪了,我高中时候学的precalculus、AP&IB calculus真的都有用么?”随着同学们题目刷的越来越多,开始接触21-25的“挑战题”时:“哇,这道概率题真是难爆了,感觉脑部带宽不够用了。”
AMC是一门真正地为了解决生活中实际问题为出发点的考试,很多时候大家学过的一个“高级”知识点会以一个不经意的方式突然“冒”了出来,get到点的同学会大呼过瘾,乃至越来越坚信数学真的是解决所有学科一切应用问题的“爸爸”。
无论是美高还是普高的数学体系下的同学们基本都学过定积分,很多同学都怀揣着一身徒手解各种不定积分题目的本事,这个技能到了大学学高等数学的时候会得到进一步提高,然后从此就再也没有然后了,若干年后,在知乎“我去市场买菜难道还要学微积分么?”的题目下狠狠地点了个“赞”。
有一些同学的答案稍好一些:“老师,定积分就是求面积。” 这个答案可以说基本正确,但是对于有强迫症的我来说,这句话看似非常正确,实则有很多毛病。那么我们来回忆一下:同学们在高中的数学课本上一般都是:为了解决不规则图形面积第一次接触了黎曼和和定积分的概念。
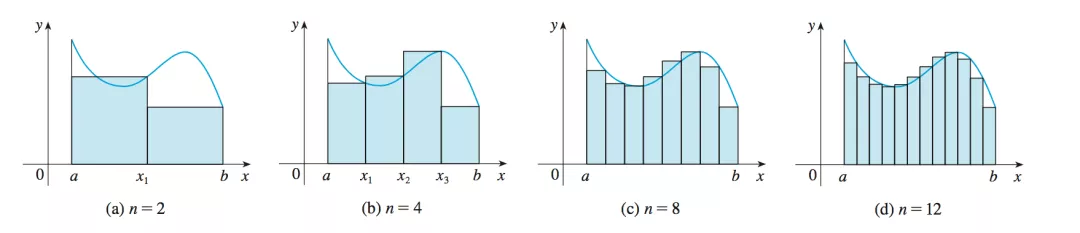
我们通过把图形的面积不断地切割成无限份,再利用近似的方式,估算出面积,并最终得到“面积”的准确算法:定积分公式。
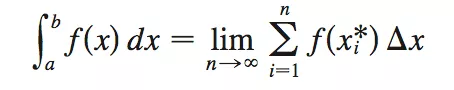
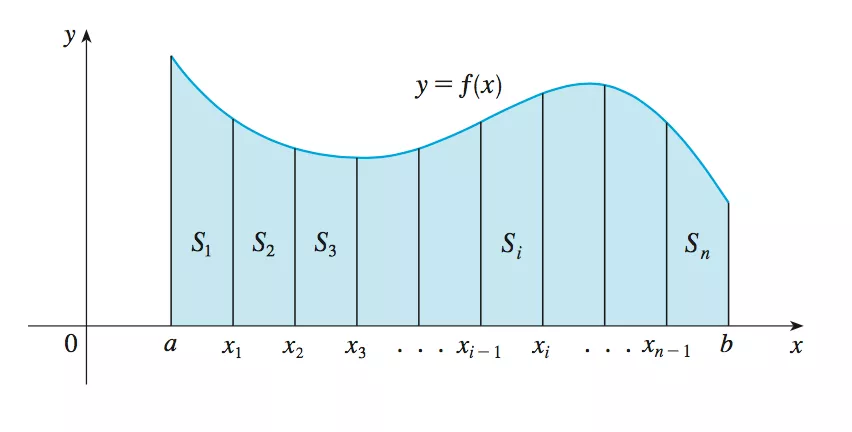
很多同学对这个知识点的理解可能到此就为止了,随后往往会把更多的时间投入到各种更难的不定积分计算中去了,甚至他们的老师往往忽视了:黎曼和求面积其实只是很狭义的一种认知,“先微小后累积”这种思想其实才是定积分的更广义的应用。
下面我们拿2016年AMC12A卷的第23题举个例子给大家看一下微积分的思想到底是如何在AMC的竞赛中出现的,它的计算相对正式的微积分考试会非常容易,但是思路更加扩展,更加“意想不到”:

这道题的题意是:
我们随机在数轴[0,1]内取三个点,以它们的数值作为三角形的三条边的边长,求问正好能够得到一个三角形的概率是多少?
大部分同学都能马上想到的思路是:
1.三角形两边和大于第三边;
2.先确立a为三个点中的最大值也就是三角形中的最长边;
3.通过independent probability求出另外两条边“打配合”大于第三条边的概率(第一条边的长度是能够确定第二条边的取值范围的)
如图所示:
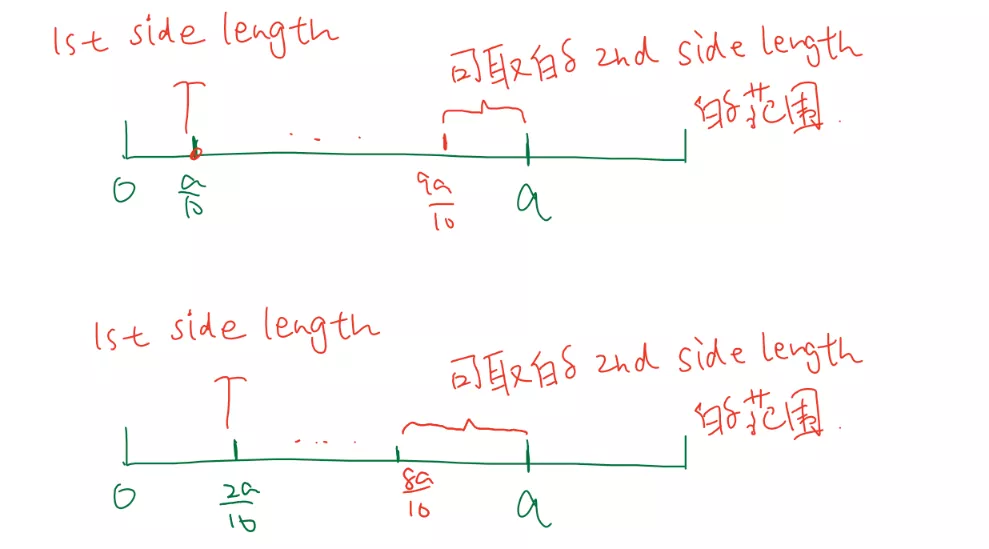
这三步是大部分同学都能想到的,但是有一个大难题横亘在大家面前:“第一条边的长度在数轴上其实只是一个点,取到每一个点的概率都为0啊,这样所有的independent probability的乘积不都是0了么?另外,该如何“穷举”所有第一条边的可能取值呢?”
如果同学们在之前的微积分学习中已经对“先微小后累积”这一思想大彻大悟,在看到这句设问时大都瞬间发现了这道题的妙处:
其实我们完全没有必要把定积分拘泥于width and length of rectangle。我们可以把第一条边的长度化一个点为一段长度“Δx”,那么第一条边的概率就可以表示成Δx/a, 第二条边的对应概率可以表示为 x/ a。
可以这么说, 第一条边的对应概率就是所谓的“width”, 第二条边的对应概率就是所谓的“length”,length*width构建出一个别出心裁的probability rectangle,接下来我只需要再求一下非常简单的幂函数积分即可:
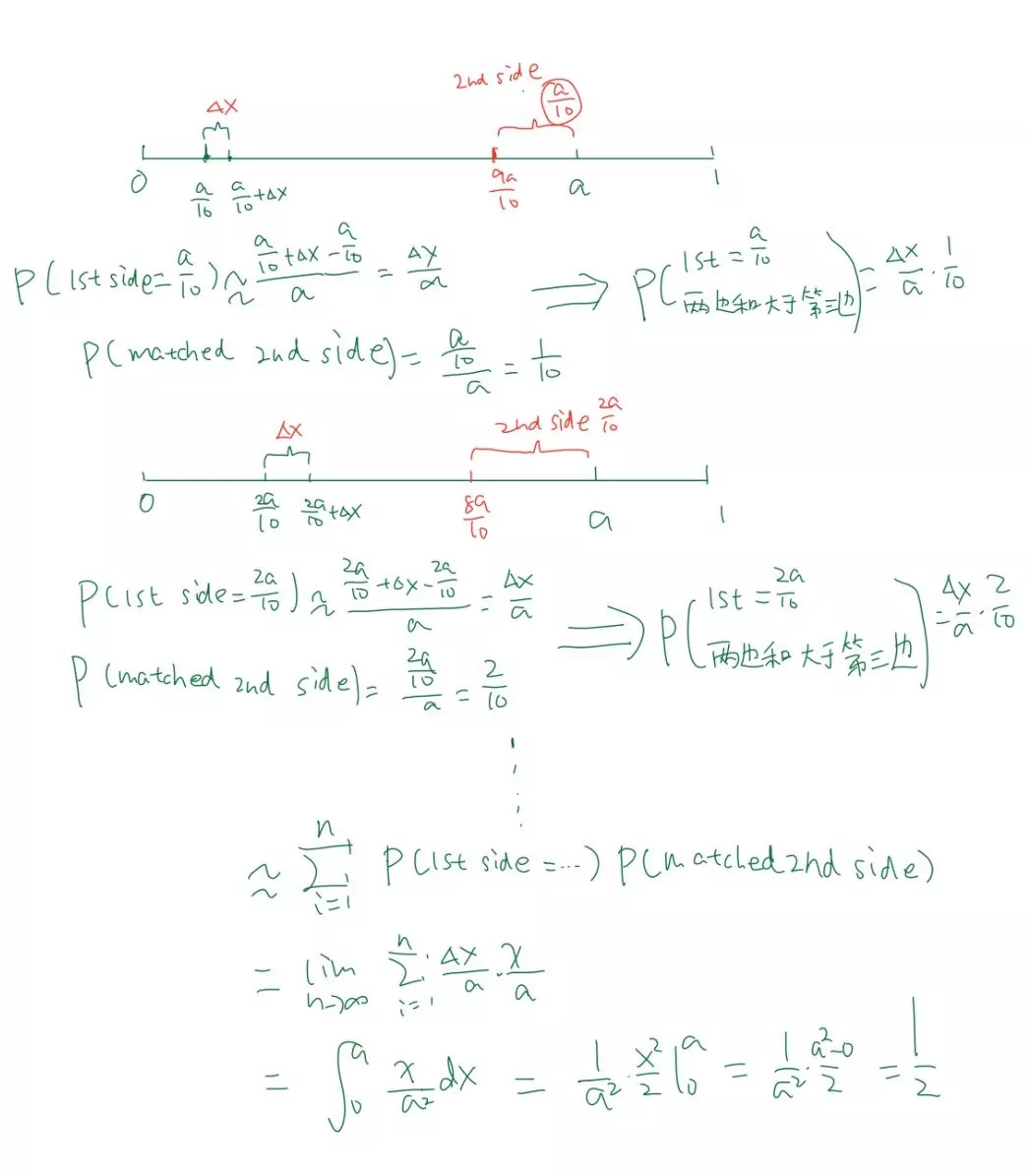
通过这一题大家可以发现一道题号为23的挑战难度题目,其实可以非常省时省力地解决,这也是我们的讲座和备考课程一直给大家灌输的思想:希望大家学习一小部分微积分的知识点,没有学过的同学不要害怕,学过的同学也不要以为自己理解得完全到位,我们并不需要特别高深的解题技巧和极快的计算速度,更需要的是对这一思想的透彻理解。
同理,还有一些数学思想,包括但不局限于统计学上离散型随机变量分布、随机过程的思想、线性代数中的矩阵运算,虽然很多都是大学的思想,但其实入门并不困难,很多时候往往能帮助我们在AMC的考试中占得一个身位的领先,我们也会在之后的文章中给大家带来更多的知识点以及考题思路的汇总和整理,更多的内容解读请继续关注……
AMC免费真题备考资料
海量AMC资源免费赠送,从此不再“资料荒”
TD学科知识竞赛教研组精心整理了包括2022年最新试题在内的历年AMC的备考真题及考试资料,精心程度请浏览下图!真正做到一次领取,考试不愁!

AMC免费赠送的备考资料
AMC真题备考资料领取方式
长按识别添加马甲微信(已经有TD小马甲的同学无需重复添加啦),并回复关键字「AMC」,即可免费领取AMC备考真题及资料,千万不要错过噢!






