
2023AP物理1北美卷——试卷整体难度和知识点
本试卷题目
整体难度不大,题目和出题情景都比较常规,
都是常见的物理模型和考法。对于转动的内容考察占比很高,有两道FRQ均以转动作为出题背景,出题更多侧重与从系统角度思考问题。
2023AP物理1北美卷——与往年题目对比
运动学和动力学单元考察的内容和形式都比较简单,只出现了斜面上的匀变速直线运动,没有出现二维的平面运动以及相关规律,实验题以斜面上的直线运动为背景,考察了图像斜率的意义。
圆周运动考察了水平面上的运动规律,以弹簧弹力提供向心力为主要考点 ,与2014的第一题十分相似,但更简单。万有引力部分和动量部分则几乎没有出题。
简谐运动主要考察了水平弹簧振子的周期公式,利用公式求解频率之比,比较简单。
能量占比例很高,虽然没有单独的题目考察,但会和不同的物理模型进行结合,并且成为贯穿题目的主线,
需要同学们深入理解功与能量的关系,并能灵活运用。
相比于2022年,这次
转动问题考察比例很高,有两道完整的题目以转动为背景,涉及到转动中的力矩的计算、牛顿第二定律、转动动能等知识,转动部分考察较为完整。
2023AP物理1北美卷——FRQ1
1.给出水平方向由小车和弹簧组成的弹簧振子系统,以及动能和弹性势能的函数图像。
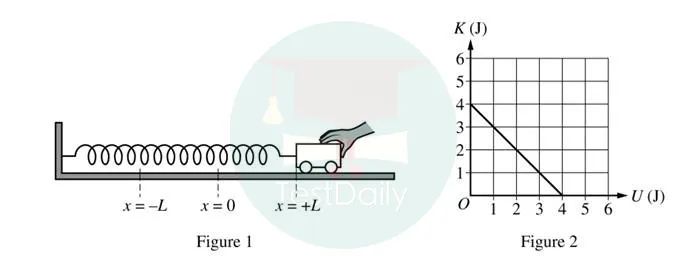
a)解释为什么K-U图像中横轴与纵轴截距应该相等。
考点:机械能守恒
思路:本题中的小车和弹簧组成的水平方向的弹簧振子系统,满足机械能守恒的条件,
故动能和弹性势能相关转化,故两种能量的最大值相同,都等于总机械能,所以截距也相同。
b)质量为原小车3倍的物块,在小车瞬时速度为0时,粘连在小车上。求组成新系统的振动频率和原有振动频率之比。
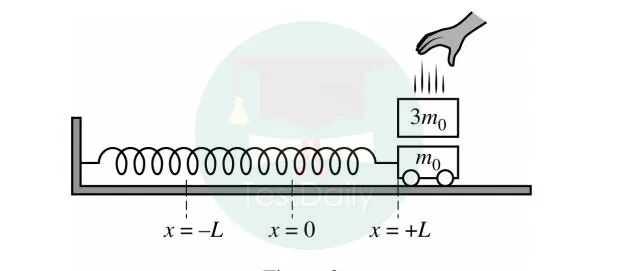 考点:弹簧振子系统的周期公式、频率与周期的关系
考点:弹簧振子系统的周期公式、频率与周期的关系
思路:利用弹簧振子的周期公式:
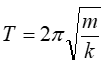
,求解出周期之比;再根据f=1/T求出频率之比即可。
c)给出新组成系统的K-U图像,i解释为什么新系统的K-U图像与原系统的K-U图像相同;ii绘制仅由小车和弹簧组成系统的K-U图像。
考点:系统机械能
思路:i小车-物块-弹簧系统与初始的小车-弹簧系统相比,没有机械能损失,故动能和势能的关系没有变化;ii小车-物块-弹簧中仅考虑小车和弹簧的机械能情况,此时最大的弹性势能不变,
但最大动能减小为1J,故图像通过(0,1)与(4,0)。
2.给出小车在斜面上的运动情景。
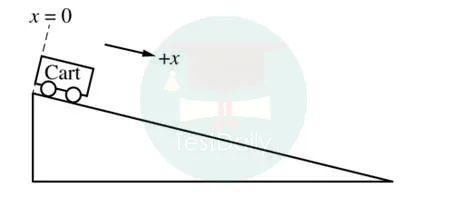
a)给出位置和时间的关系表格,i如何选取横纵轴所代表的物理量,进而计算加速度;ii根据表格数据画图;iii根据图像特点计算沿斜面向下的加速度。
考点:数据处理、利用图像特征计算物理量
思路:根据小车在斜面上做匀加速直线运动,可知
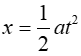
,故横轴可选

,纵轴可选x;根据表格计算出相应数据图片并画拟合图线;
利用图像的计算slope,a=2slope,注意不要用原始数据点。
b)根据实验求出重力加速度g,i由a求解g还需要知道哪些物理量;ii写出用a表达g的关系式。
考点:受力分析、牛顿第二定律
思路:
在斜面上进行受力分析,可知
,故还需要知道斜面和地面的夹角
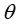
;由上

。
c)测出的g数值明显偏小,i除空气阻力和摩擦力外,什么原因使g的测量值明显偏小;ii如何减小上述误差
考点:实验分析、转动
思路:由于
车轮的转动,使小车沿斜面平动的加速度变小,
进而使g的计算值偏小;改用轻质车轮。
d)画出x-t图像与v-t图像。
考点:匀加速直线运动的规律
思路:图片,v=at,
故x-t图像为向上的抛物线,v-t图像为直线。
3.水平方向的物块在弹簧的连接下圆周运动,忽略摩擦力。

a)在不同的运动情况下,弹簧的形变量不同,做圆周运动的线速度也不同,i画出两种运动情境下物块的受力情况,ii解释i中画图特点的原因,iii判断两种运动情况下的线速度并分析原因。
考点:圆周运动、向心力、胡克定律
思路:
弹簧弹力提供向心力,由于

,所以第二个情景受力更大,画图中要有所体现;圆周运动中,运动线速度越大所需要的向心力也越大,所以第二种情况下线速度更大。
b)弹簧原长为L,弹簧的形变量为d,i根据物理量计算物块受合力情况;ii根据物理量求解圆周运动的线速度。
考点:圆周运动、向心力
思路:
根据本题中圆周运动的,弹簧弹力提供向心力。

c)b问中的公式推导结论与a中的预测结果是否相符并解释理由。
考点:圆周运动、公式推导
思路:根据公式关系,
结论相符。
4.给出转动运动的情景,滑轮的转动惯量、绳子的拉力情况以及滑轮半径。
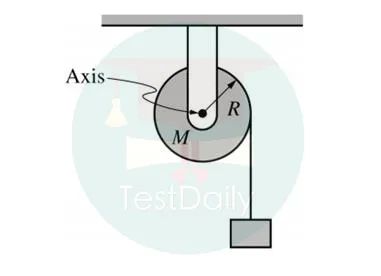
a)根据已知物理量推导角加速度。
考点:牛顿第二定律的转动形式
思路:图片,带入本题中的具体形式即可。
b)改变滑轮的质量分布,解释为何角动量情况相同,而转动动能不同的原因。
 考点:角动量、转动动能
考点:角动量、转动动能
思路:两种情境下的冲量矩相同,所以角动量变化相同,故最后的角动量相同;
由于质量分布不同,所以两种情况下的转动惯量和角速度不同,情境2的转动惯量更大,则转动动能更小。
5.质量分布不均匀的球,绕轴在竖直方向转动。
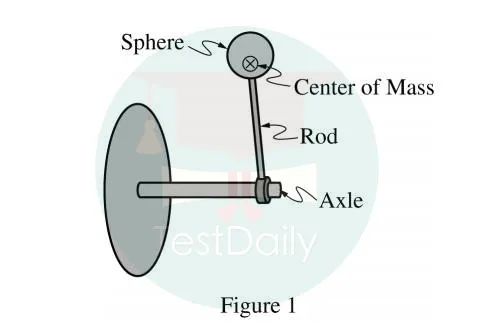
a)i选出角加速度最大的位置,并说明理由;ii选出转动动能最大的位置,说明理由。
考点:牛顿第二定律的转动形式、机械能
思路:最大角加速度出现在合力矩最大的位置,即重力矩最大的位置,故选C;最大动能出现在最低点,此时重力势能全部转化为动能。
b)i计算rod-sphere-Earth系统,从A到E的动能变化情况;ii在不考虑地球的情况下,rod和sphere为何能获得动能。
考点:机械能、动能定理
思路:重力势能转为动能,动能增加;系统中不包含地球,
则重力相当于系统外力,系统外力做功会改变系统的动能。
本文作者

福利:2023FRQ真题
TD整理了CB目前在官网最新更新的
2023年北美卷的AP FRQ真题免费分享给大家,有需要的同学可以扫下方二维码,发送
「2023frq」即可领取~其他科目真题将随官网更新陆续放入分享链接中,敬请关注~

推荐阅读
2023年AP生物北美卷考试真题及考情回顾:FRQ已放出,难度中上,数据展示有变化 |附AP北美卷FRQ真题免费下载领取!
2023年AP世界历史北美卷考试真题及考情回顾:FRQ已放出,难度提升|附AP北美卷FRQ真题免费下载领取!
2023年AP CSP国际卷考试真题及考情回顾:题型与往年类似,整体难度适中|附AP常考科目备考资料免费下载领取!
2023年AP英语语言与写作国际卷考试真题及考情回顾:难度适中,题目常规|附AP常考科目备考资料免费下载领取!
2023年AP物理C电磁国际卷考试真题/考情回顾:MCQ难度不大,FRQ考点冷门题量大|附AP常考科目备考资料免费下载领取!
 a)解释为什么K-U图像中横轴与纵轴截距应该相等。
考点:机械能守恒
思路:本题中的小车和弹簧组成的水平方向的弹簧振子系统,满足机械能守恒的条件,故动能和弹性势能相关转化,故两种能量的最大值相同,都等于总机械能,所以截距也相同。
b)质量为原小车3倍的物块,在小车瞬时速度为0时,粘连在小车上。求组成新系统的振动频率和原有振动频率之比。
a)解释为什么K-U图像中横轴与纵轴截距应该相等。
考点:机械能守恒
思路:本题中的小车和弹簧组成的水平方向的弹簧振子系统,满足机械能守恒的条件,故动能和弹性势能相关转化,故两种能量的最大值相同,都等于总机械能,所以截距也相同。
b)质量为原小车3倍的物块,在小车瞬时速度为0时,粘连在小车上。求组成新系统的振动频率和原有振动频率之比。
 考点:弹簧振子系统的周期公式、频率与周期的关系
思路:利用弹簧振子的周期公式:
考点:弹簧振子系统的周期公式、频率与周期的关系
思路:利用弹簧振子的周期公式: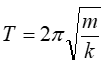 ,求解出周期之比;再根据f=1/T求出频率之比即可。
c)给出新组成系统的K-U图像,i解释为什么新系统的K-U图像与原系统的K-U图像相同;ii绘制仅由小车和弹簧组成系统的K-U图像。
考点:系统机械能
思路:i小车-物块-弹簧系统与初始的小车-弹簧系统相比,没有机械能损失,故动能和势能的关系没有变化;ii小车-物块-弹簧中仅考虑小车和弹簧的机械能情况,此时最大的弹性势能不变,但最大动能减小为1J,故图像通过(0,1)与(4,0)。
,求解出周期之比;再根据f=1/T求出频率之比即可。
c)给出新组成系统的K-U图像,i解释为什么新系统的K-U图像与原系统的K-U图像相同;ii绘制仅由小车和弹簧组成系统的K-U图像。
考点:系统机械能
思路:i小车-物块-弹簧系统与初始的小车-弹簧系统相比,没有机械能损失,故动能和势能的关系没有变化;ii小车-物块-弹簧中仅考虑小车和弹簧的机械能情况,此时最大的弹性势能不变,但最大动能减小为1J,故图像通过(0,1)与(4,0)。
 a)给出位置和时间的关系表格,i如何选取横纵轴所代表的物理量,进而计算加速度;ii根据表格数据画图;iii根据图像特点计算沿斜面向下的加速度。
考点:数据处理、利用图像特征计算物理量
思路:根据小车在斜面上做匀加速直线运动,可知
a)给出位置和时间的关系表格,i如何选取横纵轴所代表的物理量,进而计算加速度;ii根据表格数据画图;iii根据图像特点计算沿斜面向下的加速度。
考点:数据处理、利用图像特征计算物理量
思路:根据小车在斜面上做匀加速直线运动,可知 。
c)测出的g数值明显偏小,i除空气阻力和摩擦力外,什么原因使g的测量值明显偏小;ii如何减小上述误差
考点:实验分析、转动
思路:由于车轮的转动,使小车沿斜面平动的加速度变小,进而使g的计算值偏小;改用轻质车轮。
d)画出x-t图像与v-t图像。
考点:匀加速直线运动的规律
思路:图片,v=at,故x-t图像为向上的抛物线,v-t图像为直线。
。
c)测出的g数值明显偏小,i除空气阻力和摩擦力外,什么原因使g的测量值明显偏小;ii如何减小上述误差
考点:实验分析、转动
思路:由于车轮的转动,使小车沿斜面平动的加速度变小,进而使g的计算值偏小;改用轻质车轮。
d)画出x-t图像与v-t图像。
考点:匀加速直线运动的规律
思路:图片,v=at,故x-t图像为向上的抛物线,v-t图像为直线。

 c)b问中的公式推导结论与a中的预测结果是否相符并解释理由。
考点:圆周运动、公式推导
思路:根据公式关系,结论相符。
c)b问中的公式推导结论与a中的预测结果是否相符并解释理由。
考点:圆周运动、公式推导
思路:根据公式关系,结论相符。
 a)根据已知物理量推导角加速度。
考点:牛顿第二定律的转动形式
思路:图片,带入本题中的具体形式即可。
b)改变滑轮的质量分布,解释为何角动量情况相同,而转动动能不同的原因。
a)根据已知物理量推导角加速度。
考点:牛顿第二定律的转动形式
思路:图片,带入本题中的具体形式即可。
b)改变滑轮的质量分布,解释为何角动量情况相同,而转动动能不同的原因。
 考点:角动量、转动动能
思路:两种情境下的冲量矩相同,所以角动量变化相同,故最后的角动量相同;由于质量分布不同,所以两种情况下的转动惯量和角速度不同,情境2的转动惯量更大,则转动动能更小。
考点:角动量、转动动能
思路:两种情境下的冲量矩相同,所以角动量变化相同,故最后的角动量相同;由于质量分布不同,所以两种情况下的转动惯量和角速度不同,情境2的转动惯量更大,则转动动能更小。
 a)i选出角加速度最大的位置,并说明理由;ii选出转动动能最大的位置,说明理由。
考点:牛顿第二定律的转动形式、机械能
思路:最大角加速度出现在合力矩最大的位置,即重力矩最大的位置,故选C;最大动能出现在最低点,此时重力势能全部转化为动能。
b)i计算rod-sphere-Earth系统,从A到E的动能变化情况;ii在不考虑地球的情况下,rod和sphere为何能获得动能。
考点:机械能、动能定理
思路:重力势能转为动能,动能增加;系统中不包含地球,则重力相当于系统外力,系统外力做功会改变系统的动能。
a)i选出角加速度最大的位置,并说明理由;ii选出转动动能最大的位置,说明理由。
考点:牛顿第二定律的转动形式、机械能
思路:最大角加速度出现在合力矩最大的位置,即重力矩最大的位置,故选C;最大动能出现在最低点,此时重力势能全部转化为动能。
b)i计算rod-sphere-Earth系统,从A到E的动能变化情况;ii在不考虑地球的情况下,rod和sphere为何能获得动能。
考点:机械能、动能定理
思路:重力势能转为动能,动能增加;系统中不包含地球,则重力相当于系统外力,系统外力做功会改变系统的动能。













