 引言
引言
GRE数学部分的难度在于全面而深入地考察了广泛的数学知识。若想在此部分获得满分,必须拥有扎实、完备的数学知识体系;一旦漏掉了某个看似微小的概念,就有可能在考试中say bye to 170~正是基于这一挑战,我们特别为大家准备了系列文章,针对GRE数学部分的不同考题类型进行详细剖析,从而帮助大家建立起系统性的知识框架。
这个系列文章涵盖了算术、应用与图表、代数、几何和数据分析五个部分,每个部分下又细分到具体的知识点。每篇推文都将全面解读一个关键知识点,希望我们通过深入浅出的解释和丰富的例题,帮大家系统性的掌握重难点、对数学基础知识查缺补漏。我们坚信,阅读完这一系列的文章后,你会对GRE数学的考察要点游刃有余,从而在考试中取得优异的成绩~那么我们开始这一系列的第十篇推文:(几何部分)多边形吧!
之前的推文链接在这里哦:

多边形
多边形的基本概念
多边形是指由多条线段组成的平面图形,这些线段称为多边形的边,两条相邻的边会交于一点,这点称为多边形的顶点。
多边形的内角(和)、外角(和)
内角的定义:由多边形的两条相邻边所形成的角称为多边形的内角。内角和的定义:多边形的内角和是所有内角的度数之和。多边形的内角和计算公式为:内角和 = (n - 2) × 180°,其中 n 代表多边形的边数。举例来说,三角形(n=3)的内角和为180°,而矩形(n=4)的内角和为360°。外角的定义:外角是内角的补角,即与内角相邻且不重合的角。
多边形的外角和是所有外角的度数之和,为360°。也就是说,无论多边形有多少边,外角和始终为360°。对于正多边形,每个外角的度数是360°除以多边形的边数。举例来说,对于正6边形,每个外角的度数是360°/6=60°。那么正6边形的每个内角等于180°-60°=120°。

矩形的基本概念跟相关公式
矩形是一种特殊的四边形,具有以下特征:
所有内角均为直角(90度)。对边相对的两条边长度相等。对角线相等,且相交于矩形的中心点。
矩形的周长公式为:周长=2×(长+宽);矩形的面积公式为:面积=长×宽。
其中,如果相邻的边长也相等,我们可以得到矩形的特例——正方形。正方形是一种特殊的矩形,其特征除了上述矩形的特征,还包括:所有边长度相等。
正方形的周长公式为:周长=4×边长;正方形的面积公式为:边长的平方。同时,正方形的面积还可以通过对角线的平方/2来计算。

菱形的基本概念跟相关公式
平行四边形是一种特殊的四边形,其相邻边两两平行。平行四边形的周长等于所有边的长度之和,面积为底边长度和高的乘积。除了刚才提到的矩形、正方形属于平行四边形之外,菱形也是一种特殊的平行四边形,菱形具有以下特征:
1.所有边长度相等。2.对角线相等且垂直于彼此。
菱形的周长等于四条边的长度之和,周长公式为4×边长;菱形的面积公式为:两条对角线的乘积/2.

例题
例1

解:
由题意可知,P1是五边形,根据4.1.2的知识,五边形(n=5)的内角和为(5-2)*180°=540°;P2是十边形,同理,它的内角和为(10-2)*180°=1440°。Quantity A为P1内角和的两倍,也就是1080°,小于Quantity B。
因此本题选B。

例2

解:
因为这个图是中心对称,所以四个角上的三角形是全等的。从右边的x我们得知每个三角形的底、高之和为x;从z得知每个三角形的底为z;因此,每个三角形的高为(x-z)。同时,因为内部的正方形边长为y,我们得知每个三角形的斜边为y。根据直角三角形有的勾股定理,我们得到选项E。
例3

解:
这道题目第一步可以根据正方形ABCD的面积算出CD=25。CDEF是菱形,所以DE=DC=25。此时我们需要注意,尽管题目中提到CDEF是菱形,我们不能被菱形面积计算公式的思维定势扰乱做题思路~第二步我们可以发现,CDEF作为一种特殊的平行四边形,它的面积同样可以用底*高来计算。因此,我们可以得到CDEF的高为20。
因此,我们可以做如下的辅助线:
例4
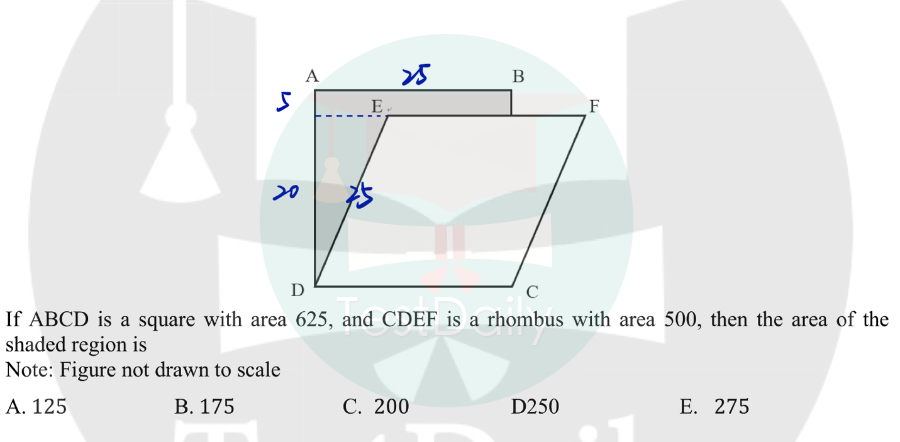
我们可以通过直角三角形的勾股定理来计算图中三角形的底为15。现在,我们可以较为轻松的计算阴影部分的面积。具体来说,阴影部分的面积=三角形面积+矩形面积=20*15/2+5*25=150+125=275。因此答案选E。
结语
这篇推文包括了GRE数学在(几何部分)多边形范围内的大部分考点。我们会把三角形的考点放在下一篇推文里详细说~我们需要知道:
1、多边形的基本概念;2、多边形的内角(和)、外角(和);3、矩形的基本概念跟相关公式;4、菱形的基本概念跟相关公式。
那么希望看到这里的你能查缺补漏,有所收获~

福利&领取方式
厚朴GRE还特别为大家准备了备考GRE所需要的全部资料,赶紧戳小马甲并发送暗号「GRE干货群」即可入群获取全部资料啦~









