把图形分割成长方形
说起积分，就必须要提到一个人：德国数学家波恩哈德·黎曼。各位同学正在学到的“Riemann Sum（黎曼和）”就是以他的名字命名的。 黎曼和出现的原因说来很简单，人们想要去计算一块形状不规则的土地面积，但当下能用的面积计算公式只能计算长方形、三角形等规则几何图形的面积，这时候怎么办呢？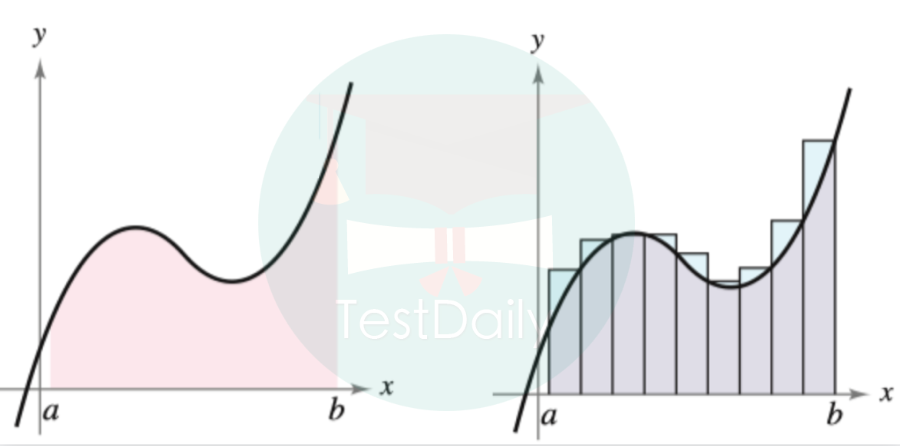
黎曼想了一个办法：将形状不规则的土地切割成一个一个的细长条，然后将每一个细长条地看做长方形，再测量出每一个长方形的面积，把这些长方形的面积加起来就可以得到形状不规则的土地面积的近似值了，这就是著名的黎曼和。
在分割细长条的过程中，如果分割的小长条数量越多，则每个小长条的宽度越小，这时长方形的面积之和就会越接近实际的土地面积。各位同学在微积分课堂上学到的左黎曼和、右黎曼和以及中点黎曼和便是基于这种思想而产生的更为系统化的估值方法。
初识黎曼和——求圆的面积
其实同学们在听到黎曼和这个词之前就已经在学习和使用它了，例如求圆的面积。 我们现在非常熟悉的圆其实也是一个复杂的图形，如何准确地求出圆的面积在很久以前并不是一个简单的问题。很多同学对圆的面积探究应该始于小学数学课上“数方格”的方法，即用圆规在方格纸上画一个圆，然后数出圆中方格的个数，用正方形的面积之和来近似圆的面积。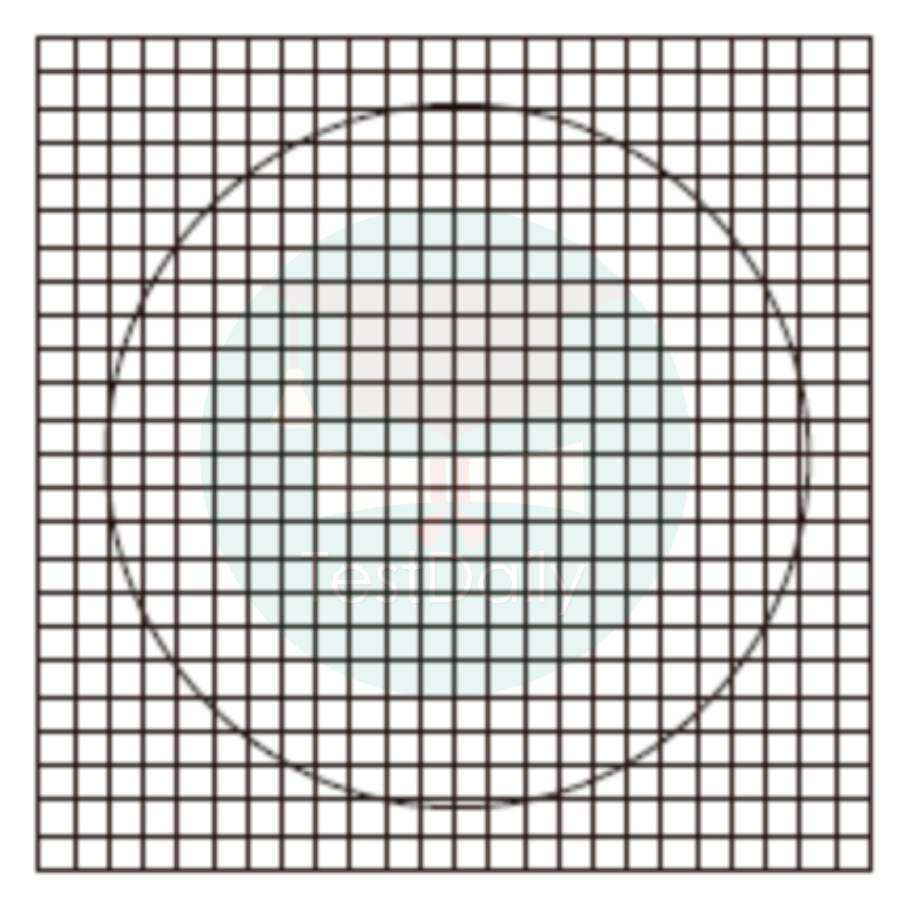
那如果我们想让正方形的面积之和尽可能地接近圆的面积又该怎么做呢？回想我们前面提到的测量不规则形状土地面积的方法，如果我们让方格纸上的方格变小，方格数量变多，那么这时正方形的面积和是不是就会更接近圆的图形面积？
从图中我们可以看出，粗糙的图形变得越精细，它就会越接近实际的圆形。由此我们可以知道，要想求出一个圆的面积，就需要我们能够很精细地分割圆形，而分割的形状并不局限于正方形，我们也完全可以把圆分成很多细长条，利用长方形的面积来求出圆的面积。
具体操作如下：首先我们可以把圆放在平面直角坐标系中，沿着y轴的方向把圆裁剪成很多很细的长方形，之后我们可以在众多的长方形中找到一条宽度为△x的细长条。在微积分中我们一般用它表示非常小的数值，读作delta x。
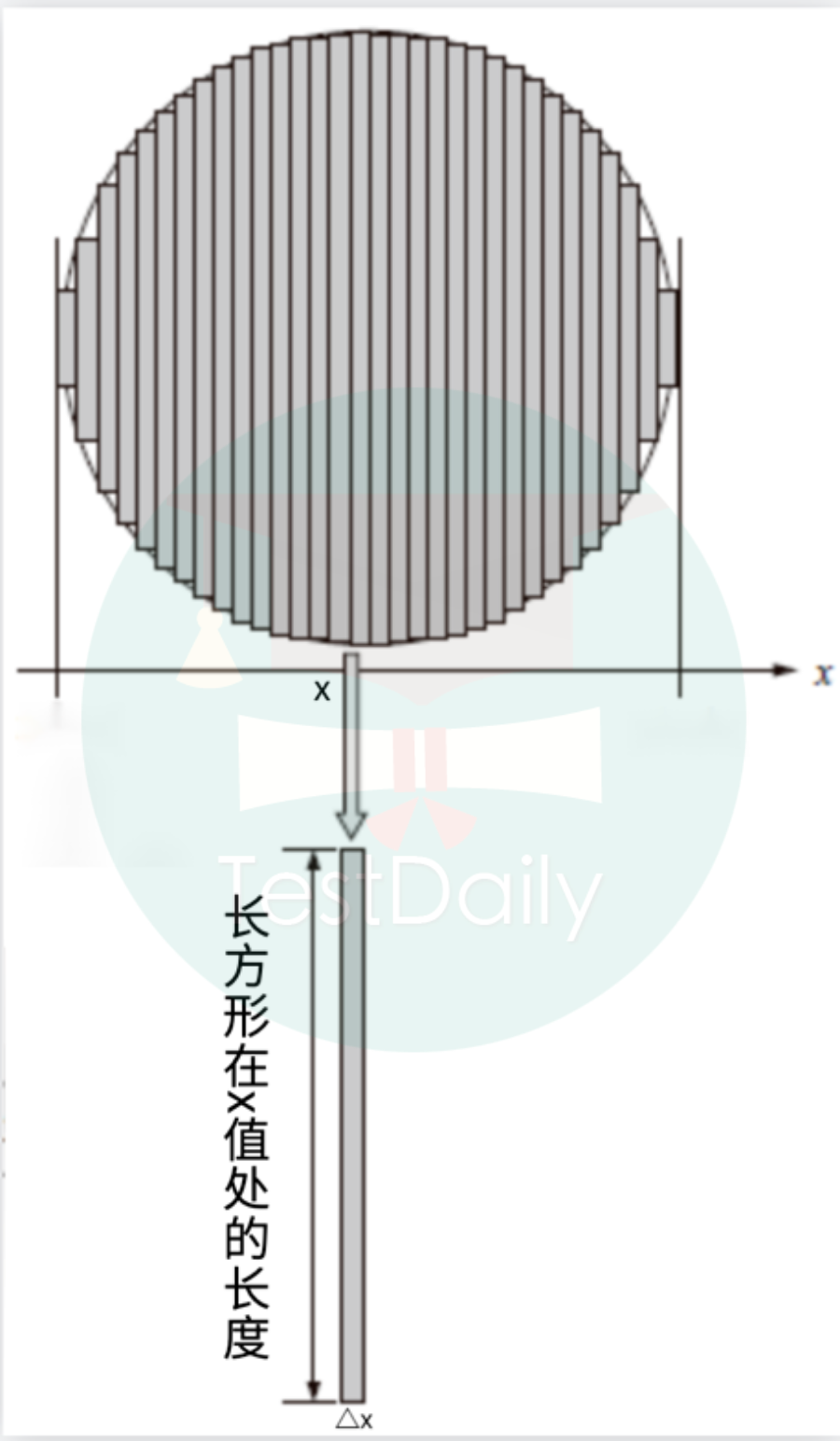每个细长条的面积是非常容易就能得到的：（长方形在x值处的长度）*Δx，之后我们可以对分割出的其他长方形进行同样的运算，得到全部长方形的面积，最后再求和便可以得到一个接近圆的真实面积的数值。
这时我们得到的数值只是一个圆面积的近似数值，如果我们想得到圆的真实面积则需要继续精细地分割图形，即缩短长方形的宽度，以此增加长方形的数量，从而让长方形的面积之和逐渐逼近圆的面积。
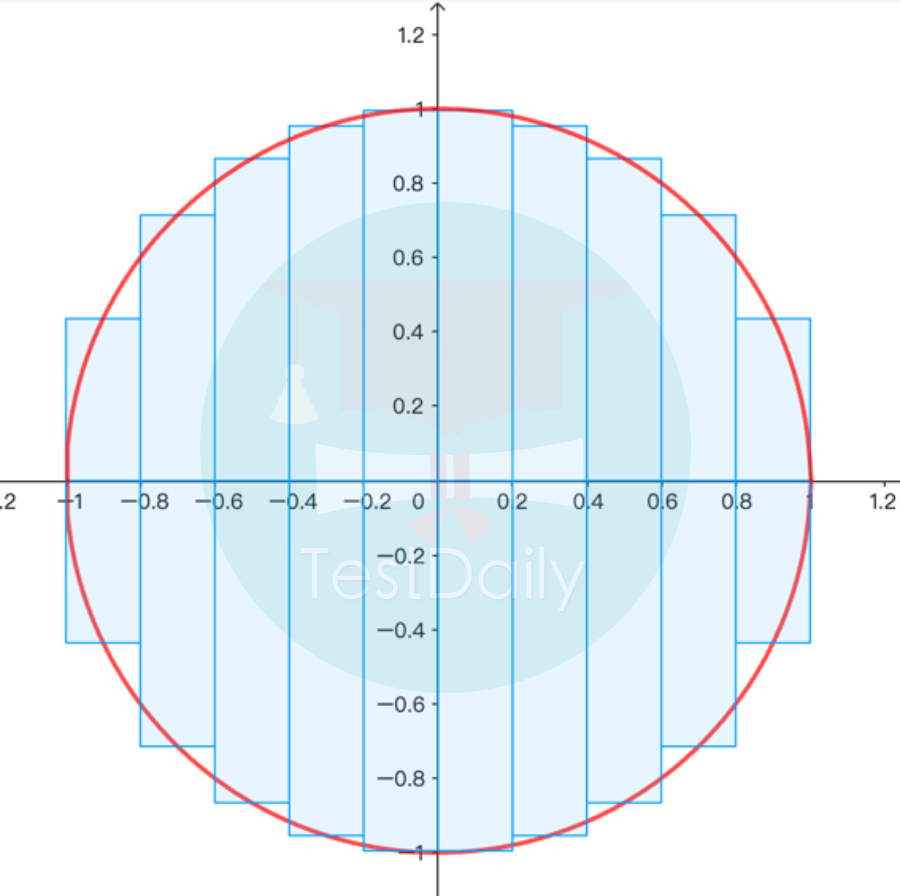如果用numerical method来展示也会更加清晰，我们可以用圆心坐标（0,0）半径为1的圆来感受一下此种估值方法。
首先，从x=-1到x=1的总长度为2，我们在这一段上分出n个宽度相同的长方形，则每一个长方形的宽度为
利用计算器我们可以一次计算出n取不同数值的时候，长方形面积的总和。
在上面的表格中，我们把长方形的数量从10增加到10000，宽度则从0.2减少到0.0002，对应的长方形面积和则从3.17198逐渐减少到3.14159，结果有着逐渐接近3.1415926…=π的趋势。
此外，虽然宽度为0.0002的长方形已经非常纤细了，但它并不是我们在分割图形时可以选择的最精细的尺寸。我们如果想要得到真实的图形面积，我们可以利用极限的思想，让长方形的宽度继续减小，逐渐逼近0。利用这种方法，我们不仅可以计算出圆的面积，也可以计算出形状更不规则的图形面积。
更高维度的应用——求体积
如果我们将黎曼和估值的思想应用在三维空间中，我们还可以计算出不规则立体图形的体积。 我们可以将不规则立体图形分割出很多三维版的细长条，这时可以利用长方体的体积来计算一个细长条的体积，求出全部长方体体积之和便可以得到实际立体图形体积的近似值。再借助极限的思想，让分割出的长方体底面积越来越小逐渐趋近于0，便可以得到实际图形的体积。 当然了，在AP微积分的学习中，我们暂时不会见到下图这样复杂的例题图形，等各位同学学到了多变量微积分便会逐渐接触到更高维度的问题。
写在最后
对于正在学习微积分的同学而言，微分和积分的计算并不仅仅局限在简单的公式套用上面，各类概念的引入和公式的推导都是在让我们习惯于用严谨的逻辑思考来获得结论。同时，将思考应用于实际，用自己的力量将理论知识于实际生活结合在一起，长期下来不仅可以锻炼我们的逻辑思维能力，也可以帮助我们发现隐藏在数学关系背后的自然现象的本质。本文作者
TD福利&领取方式
为帮助同学们拿下AP微积分BC的5分，我们准备了AP微积分求导积分100题，免费！送给！大家！再也不用因为遇到难题却想不起来怎么做而抓马了！
AP微积分求导&积分100题封面预览
有需要的同学可以扫描下方二维码，添加TD小马甲（已经有TD小马甲的同学无需重复添加啦），给马甲发送暗号「求导积分」即可领取~
推荐阅读
