一、2023 AMC12B试卷分析
2023 AMC12B考试题中，代数与函数有6道，复数1道，几何9道，概率3道，其中2道古典概型实际是考察计数，计数1道，数论3道，另有逻辑推理1道，统计1道。
二、考题分析
1、代数与函数
共6道题，总题量适中，以简单题与中低档题为主，对数考察了一道，抽象函数考察了一道。与2023 AMC12A比，题量减少，且总难度降低。 第1题考察比例计算。 第2题考察百分数计算，涉及折扣，是经典问题。 第6题考察高次不等式求解，也是经典方法，2020 AMC10A第17题考察过该方法。
第7题涉及了对数，主要是分式不等式解法，方法与第6题相同。
附2020 AMC10A第17题
第14题考察韦达定理，涉及到整数的分解，本身不难。
2021春AMC10A第14题，AMC12A第16题方法与本题类似，考察的是六元韦达定理，且要求更高，综合性更强。
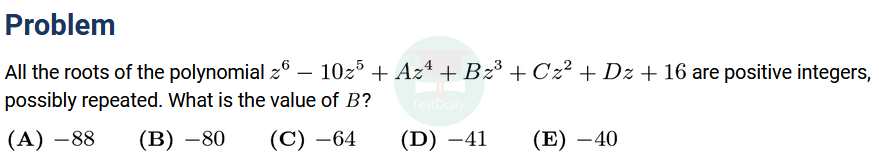第22题考察抽象函数，位置属于高档题，但方法指向很明确，赋值法，对有过此类问题研究经验的考生来说比较轻松。
2、复数
1道题，第12题，考察模长，本质是一个方程组求解问题。3、几何
共9道题，平面几何5道，解析几何2道，立体几何2道，与2023 AMC12A对比，题量增加，难度也有增加。 第3题平面几何，考察固定结论，直角三角形的外接圆直径即为斜边。 第4题平面几何，考察矩形面积，涉及单位换算，基础题型。 第9题解析几何，考察不等式表示的平面区域，中档题型，也属于固定类型题目，在此方面接触较少的同学做起来不太顺利。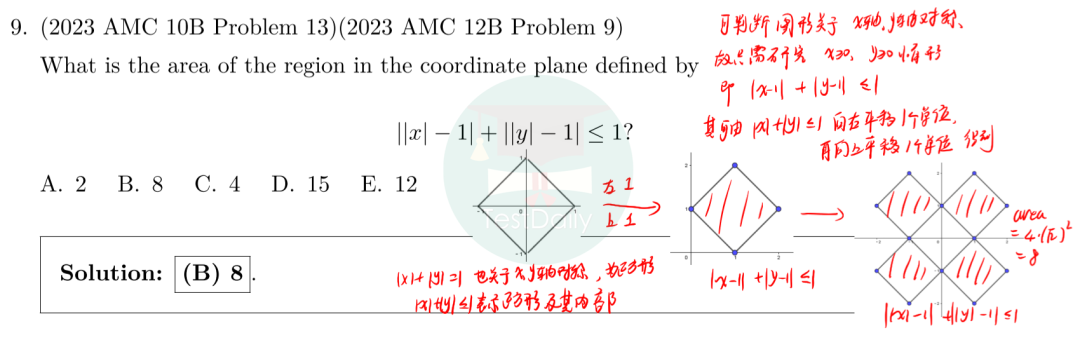
2016 AMC12B第23题考过一个类似方法，不过是立体几何。
第10题解析几何，求两圆相交弦的斜率，考察平面几何中两圆位置关系的结论，相交两圆的圆心连线垂直平分相交弦，所以找到圆心坐标，求出圆心连线斜率，再取负倒数即为所求，算中低档题。
第11题平面几何，考察等腰梯形面积最大值，与二次函数结合的经典问题类型，考察等腰梯形辅助线，作双高，中档题型。
第13题立体几何，考察长方体中的经典计算，包括棱长，体对角线，表面积等，同时结合了(a+b+c)2=a2+b2+c2+2ab+2bc+2ca，也是经典问题。
第17题平面几何，涉及等差数列，主要考察余弦定理，列式解方程后即可求出三角形面积。
第21题立体几何，考察圆台的侧面展开，题目类型为立体几何中经典最短路径问题，中高档题，综合性较强。
第25题平面几何，考察正五边形计算，相似图形面积。本题虽然在第25题位置，但其实2015年AMC10B的第22题的图形就是本题要的图形，而且要用的结论一致。
下题图中的ABCDE即为25题中的正五边形，按其描述折叠后得到的是正五边形FGHIJ，图中会出现两类等腰三角形，36°-72°-72°与108°-36°-36°，其中前者称为黄金等腰三角形，因为可以根据相似三角形求得其底与腰的比值为黄金分割比例(√5-1)/2，如果知道这个结论，很容易求得新正五边形的边长是原正五边形边长的[(√5-1)/2]^2倍，面积则为原正五边形的[(√5-1)/2]^4倍。
4、概率、计数与数论
除第8题相对靠前外，其他题目在15及之后，难度相对较高。 ?概率部分 第19题与第23题考察古典概型，但实际考察的是计数方法，其中第19题的计数方法是隔板法的变式，需要有相应的方法储备才能识别出来。 第20题考察几何概型，所用为经典方法，同时涉及到相交两圆的处理。
?计数部分
第8题为求集合满足条件的子集个数，直接按集合中元素个数（或者最小元素）分类讨论即可。
?数论部分
第15题考察的线性不定方程，本题将原方程化为15a+14b=c后，利用两边除以2，3，5，7的余数分析即可。
其实本题有一般结论，关于线性不定方程ax+by=c，当且仅当d=gcd(a,b)|c时方程有整数解，否则方程没有整数解，并且还可以根据特解(x0,y0 )得到通解(x0+bt/d,y0-at/d)（是一个整数）。
第16题考察整数的线性组合，问题转化为不能用6的正倍数，10的正倍数，15的正倍数组合出的最大正整数，可通过举例子，或者通过研究余数可以得到结果。
第24题考察最小公倍数，题目所给条件隐藏了a,b,c,d 4个数的质因分解中2，3，5的power的信息，本题方法与2016年AMC10A第25题12A第22题一致。
5、其他
第5题是逻辑推理，通过举例尝试可得到结果。 第18题考察平均数，题目给的信息比较多，且无法算出确定结果，主要考察的一个结论是两组数据混合后的平均数，介于原两个平均数之间，这样就很容易锁定答案是A。三、与往年对比
1、与2023 AMC12A卷对比
相比A卷，2023 AMC12B在整体难度上持平，主要体现在前边中低档与中档题目的难度，在考察内容上，和难点设置上有调整：1.B卷考察内容多了逻辑和统计，增加了逻辑推理1道和统计中平均数1道，且后者在18题的位置，对学生并不友好。 2.内容占比有调整： 代数与函数占比减少：A卷有11道，B卷只有7道 几何占比大大增加：A卷4道，B卷11道 3.难点设置上，A卷以代数为主，也有计数与概率，B卷比较均衡
2、与往年对比
整体题型与涉及知识点的范围与往年区别不大，不同的地方主要体现在题目难度的变化，主要是在中高档题目（评分为4分）的难度有所降低，难题（评分为5）的题目数量减少。 与去年题目相比，整体难度下降比较明显，尤其是基础题与中档题，对于各梯队的学生来说都比较友好，而且从知识与方法的考察来说，更加考察学生的知识储备量。四、备考建议
结合2023 AMC12的AB卷考法考点，对比往年题目，可以看到，代数与函数、几何仍然是核心的两大板块，占了较大比重，基础，中档，高档题目都有涉及，也是对知识储备量的一个考察，在复习时，基本结论要熟练掌握，也要尽可能多地积累经验，题型和方法。 其次，计数概率与数论，一直以来是竞赛中的难点，对于考生来说，是必然要花一定时间复习，至少要解决中15及以前的问题，对于追求高分的同学，则要研究高档题目的处理。 另外，对于统计，逻辑等内容，也要作一定的针对复习。
本文作者
推荐阅读
