2023年BMO数学竞赛考情分析:BMO比前两年略难,考点分布全面!|附BMO历年真题免费下载领取!

随着上周BMO考试的结束，下半年英美两大数学竞赛也宣告落下帷幕。BMO作为英国选拔IMO选手的预选赛，其也成为了许多学生证明数学能力的最佳选择之一，下面我们就来一起跟随TD竞赛教研组老师的分析看看2023年BMO Round1的整体情况吧。

整体评价、考点分布

2023年度BMO考卷6道考题考点分布情况为数论1道、几何2道、代数1道以及排列组合2道，四大知识板块都有涉及，考点分布全面，具体的考点分布见下表：

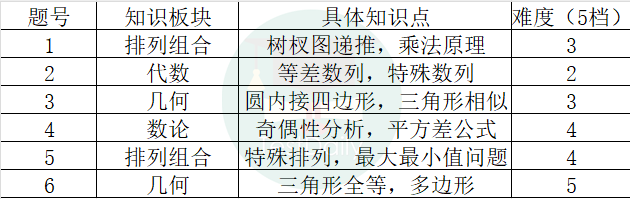
从难度上讲，本次试卷比前两年略难，前两年都有比较容易的送分题，而本套试卷从第1题起每道题都需要竞赛基础和一定的思考过程。整套试卷虽然略难但整体的难度梯度还是存在的，对于各分数段同学预期规划的每题考试时间还是基本不受影响，可以把更多的时间放在自己的分数段应做的题号上。

题目详解与对比

第一题：

?解析：

每个字母最多往后排一位，往前排无所谓，所以我们倒序思考，比如ABCD，4个字母有多少种方法：

从例子中可以总结，一共n个字母，最后一位（第n位）有两种选择。选好后的倒数第二位（n-1位），会新增一个字母选择，同时也少了一个选择（第n位的字母不能再选），还是两种选择。因此，第n位倒推至第2位都是两种选择，第1位只剩唯一的选择，共2n-1种选择。当n=9时，共256种选择。

本题的关键在于通过对小数例子的分析找到规律，发现倒序思考比较好解，这种从小例子发现规律的方式在此前的试卷中多次出现，也是我们BMO课堂上多次示范的方法。第二个要点就是树杈图式的递推方法，树杈图式的应用我们在2020年第3题、2013年第4题等题中都有见过，总体而言对于第1题是较难的。

第二题

?解析：

本卷第2题是数列题，第一种情况就是等差数列的变式，这种形态的处理在竞赛中算常规的；第二种略难，特殊数列递推公式的处理需要同学仔细观察式子结构以及发散思维，虽然每个递推各不相同，但这点基本逻辑是不变的。

第三题：

?解析：

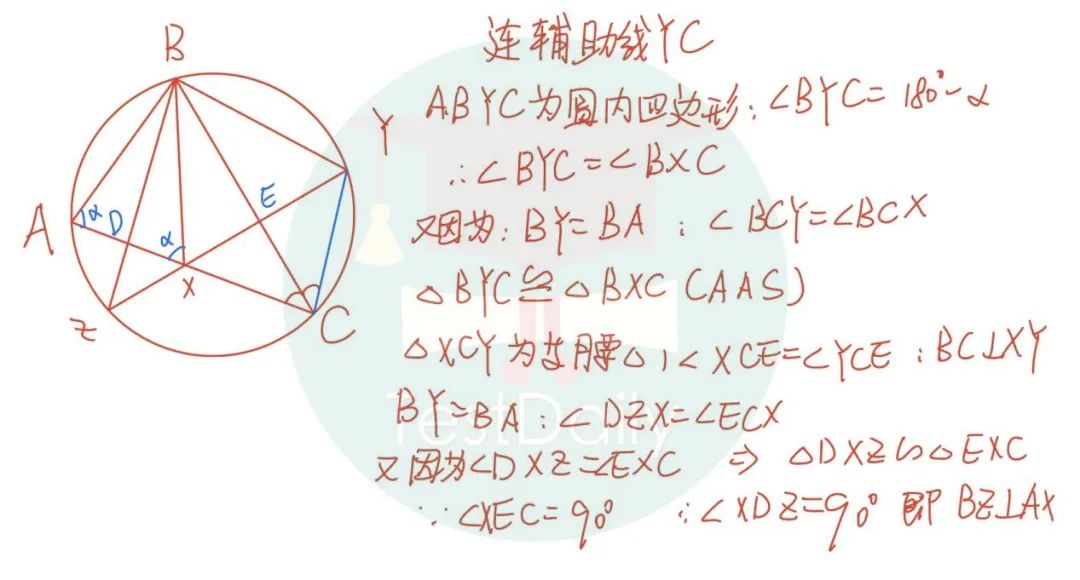
从05年至今年除了17年其他年份都有圆的几何题，BMO关于圆的考察，圆的内接四边形对角互补以及外角等于内角的对角是高频考点，今年也不列外，依旧用到了四边形内角互补，进而证明三角形全等和相似，总体来说几何体非常常规。

第四题：

?解析：

第4题是平方差公式结合奇偶性讨论的数论题，这两点在往年诸多题目中均有考察如14年第2题、06年第6题等，也是高频考点，只要仔细备考过的同学对这些分析都不会陌生，本题亮点是后面可以结合不等式进行n的范围确定。

第五题：

?解析：

按照题目要求，我们最多能找到4个连续排列不出错的方式：RBBR，而其他的15种4个连续的排列至少有一个错误，这点可以通过枚举来说明，也就意味着，用其它方式排列，至少会出现1000/4=250处错误。

接下来我们看RBBR的情况错误能否更少，RBBR本身没有错误，但它后面无论是接R还是B都会产生错误，所以它的错误产生在连接处，1000个珠排成圆，4个一组，会有250处连接，因而也至少产生250处错误。

第5题这种类型的题目是BMO区别于其他数学竞赛的特色题目，借几何中的排列组合为背景，最后落点在最大最小值问题上，22年第4题、17年第5题都是这样的出题路数。很多同学碰到这类题没思路，其实是有答题套路的：基本都是先算一个理论的最大最小值，再给一个实际操作方法。其中第一步还是比较容易拿分的，考虑极限的情况即可得知最大最小值，而第二步的操作往往是各题都不一样，是题目难点。