GRE数学考点类型讲解带练之“正态分布、数列”|附GRE备考干货免费下载领取!

引言

GRE数学部分的难度在于全面而深入地考察了广泛的数学知识。若想在此部分获得满分，必须拥有扎实、完备的数学知识体系；一旦漏掉了某个看似微小的概念，就有可能在考试中say bye to 170～正是基于这一挑战，我们特别为大家准备了系列文章，针对GRE数学部分的不同考题类型进行详细剖析，从而帮助大家建立起系统性的知识框架。

这个系列文章涵盖了算术、应用与图表、代数、几何和数据分析五个部分，每个部分下又细分到具体的知识点。每篇推文都将全面解读一个关键知识点，希望我们通过深入浅出的解释和丰富的例题，帮大家系统性的掌握重难点、对数学基础知识查缺补漏。我们坚信，阅读完这一系列的文章后，你会对GRE数学的考察要点游刃有余，从而在考试中取得优异的成绩～那么我们开始这一系列的第十四篇推文：（数据分析部分）正态分布、数列吧！

之前的推文链接在这里哦：

正态分布

正态分布的基本概念

正态分布是具有两个参数μ和σ^2的连续型随机变量的分布：第一参数μ是遵从正态分布的随机变量的均值，第二个参数σ^2是此随机变量的方差。遵从正态分布的随机变量的概率规律为取μ邻近的值的概率大，而取离μ越远的值的概率越小；σ越小，分布越集中在μ附近，σ越大，分布越分散。

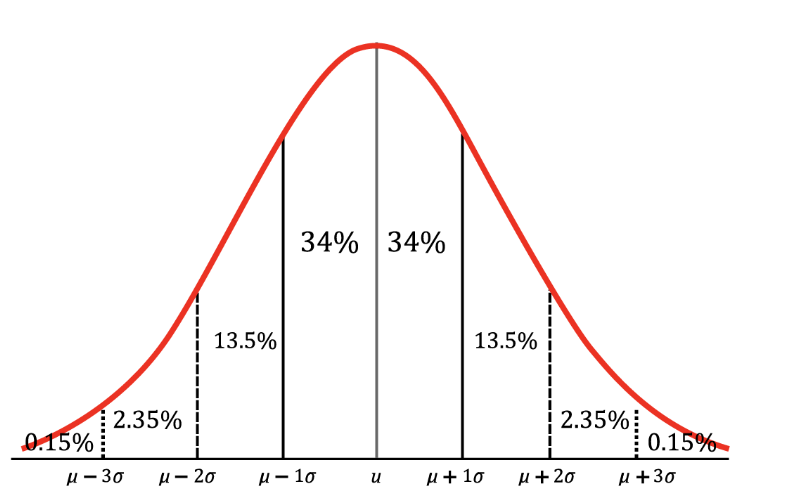
正态分布的密度曲线是类似下图的“钟形曲线”：

正态分布的经验法则

正态分布的经验法则（Empirical Rule）有时也称为 68-95-99.7法则。

根据经验法则预测：在正态分布中，68% 的观测值落在第一个标准差（µ ± σ）范围内，95% 的观测值落在前两个标准差（µ ± 2σ）范围内，99.7% 的观测值落在平均值的前三个标准差（µ ± 3σ）范围内。也就是说，对于正态分布数据，几乎所有观测数据都会落在数据平均值的三个标准差之内。考试中会重点考察这条法则～

👉例题1

解：

根据等式220=200+2*10=µ + 2σ我们得知：观测值220是均值（200）右侧的第2个标准差（10），因此根据正态分布的经验法则，观测值220右侧还有大约（1-95%）/2=2.5%个观测值，小于1/6=16%。因此这道题目我们得到答案B。

👉例题2

解：

根据正态分布的经验法则，15th percentile的观测值大约在左侧第2个标准差跟第1个标准差之间，因此我们可以得到这样的不等式：µ – 2σ<观测值<µ – σ。代入µ=470，观测值=340，我们得到σ的取值：65<σ<130。因此这道题目我们得到答案A。

👉例题3

解：

根据166=158+8= µ + σ，我们知道观测值166是均值（158）右侧的第1个标准差（8），因此根据正态分布的经验法则，观测值166右侧还有大约（1-68%）/2=16%个观测值。题目中提到data size为1000，因此166右侧的数共有1000*16%=160个。因此这道题目我们得到答案A。

数列

数列的基本概念

数列是一列有序的数，数列中的每一个数称为数列的项（term）。

面对数列：1，2，3，4，5，…我们可以得知：

1、1是第一个项，2是第二个项，3是第三个项，以此类推。

2、数列中的项通常遵循某种规律或模式，我们可以通过找规律来预测数列中的未来项。这个数列中每个项都比前一项大1，所以这是个等差数列。因此，对于数列中的第n项，它的值就是n本身：第10项是10，第100项是100…

👉例题1

解：

通过找规律，我们发现当项数是3的倍数时，该项的值为4。因此，150th term的值为4，151th term – 154th term的值为1，-3，4，1。题目需要求150th term-154th term的值的和，即为4+1-3+4+1=7。因此这道题目我们得到答案7。

👉例题2

解：

根据题意，我们需要求数列-90，-89，-88，…，-1，0，1，…，88，89，90，…，95的和。通过找规律，我们发现-90，-89，-88，…，-1，0，1，…，88，89，90这一部分可以相互抵消。因此，题目的要求转化成了求91+92+93+94+95的和，为465。因此这道题目我们得到答案C。

👉例题3