
一元二次方程介绍
高等数学(advanced math)中解一元二次方程(solving quadratic equation)是每次考试的必考知识点,也是整场考试中相对较难、计算量较大的知识点,很多同学都会在此丢分。一元二次方程的解法有很多,考试过程中选择最简便、契合的解法能够帮助我们提升做题的速度和正确率,今天就跟大家聊一下如何解一元二次方程。
一元一次方程基础知识讲解
常用的解一元二次方程的方法有以下几种:
因式分解法
配方法
求根公式
除了以上三种方法外,还有另外两个在考试中快速做题的小方法,那下面就让我们一一学习一下。
1.因式分解法
当二次方程可以因式分解为两个一次因式的乘积时,就可以使用因式分解法求解。
下面是使用因式分解法解二次方程的一般步骤:
将方程写成一般形式:将二次方程写成图片的形式。
尝试因式分解:尝试将方程进行因式分解,将其写成两个一次因式的乘积形式。
令每个因式等于零:将得到的两个因式分别设置为零,然后求解得到每个因式对应的x的值。
?让我们通过一个例子来说明因式分解法的步骤:
已知方程x2-5x+6=0
将方程写成一般形式:
x2-5x+6=0
尝试因式分解:
观察常数项6,我们需要找到两个乘积等于常数项6、和等于一次项系数-5的数,-2和-3符合条件,因此我们可以将方程因式分解为(x−2)(x−3)=0。
令每个因式等于零:
分别令x-2=0和x-3=0,解得x=2和x=3。
因此,方程x2-5x+6=0的解为x=2和x=3。
因式分解法通可以帮助我们快速找到二次方程的解,但并不是所有的二次方程都可以简单地进行因式分解,我们需要根据具体题目来决定使用什么方法。
2.配方法
当ax2+bx+c=0的二次项系数a为1时,就可以使用配方法来解方程。这种方法通过将二次项与一次项配对、构造成完全平方的形式来求解。具体步骤如下:
确定a为1:首先确保二次项系数a为1,如果不是,则需要将整个方程化成a=1的形式。
配方:将c移到等式右边,再将一次项系数b的一半的平方加到等式的两边,这样可以使得等式左边成为一个完全平方的二次项,等式右边是一个常数。
完全平方的形式:将等式左边写成完全平方的形式。整个二次方程变成完全平方式等于常数的形式。
解方程:将等式两边同时开方求解,从而得到方程的解。
?让我们通过一个例子来说明配方法的步骤:
已知方程x2-8x+5=0
确定a为1:
该方程a=1,符合要求。
配方:
将-5移到等式右边,等式两边同时加上16(8除以2的平方)得到:
x2-8x+16=-5+16
完全平方的形式:
(x-4)2=11
解方程:将等式两边同时开方求解,得到x-4=±√11,解得x=4+√11和x=4-√11。
因此方程x2-8x+5=0的解为x=4+√11和x=4-√11。
配方法也是常用的求解二次方程根的方法,但是二次项系数不为1或者一次项系数为分数时,配方会变得麻烦。有时配方完成后等式右边的常数项为负数,此时方程的根会是一个复数。所以在未来求解的过程中,面对不同的题目应该选用合适的方法。
3.求根公式法
对于方程ax2+bx+c=0
当b2-4ac>0时,我们可以直接用求根公式来求出方程的两个根:

?比如下面这个例子:
对于二次方程2x2-3x-4=0
a=1, b=-3, c=-4
代入到求根公式中:
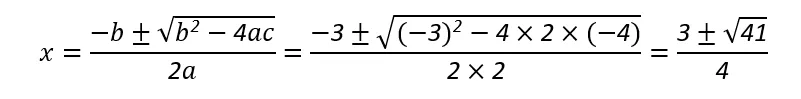
求得方程的根为:

在使用求根公式时,很多同学都会因为漏掉公式中-b前面的负号、或是代入系数时漏掉系数前面的负号导致计算错误而丢分,因此在考试中需要特别仔细小心。
4.韦达定理
韦达定理是一个用于解决二次方程根之间关系的方法,也被称为韦达方程。
该定理表述如下:
对于二次方程ax2+bx+c=0。它的两个根和之间有以下关系:
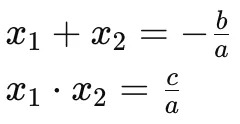
这两个关系在我们求解二次方程时,即使我们不知道根的具体值,也可以根据这些关系得到它们之间的关系。
比如对于方程2x2-5x+3=0,根据韦达定理,我们可以知道:

因此方程2x2-5x+3=0的两个根的和为5/2,乘积为3/2。
在考试中,很多题目不会让你求出两个根分别是多少,而是让你求两根之和或者两根之积是多少,这个时候我们就可以运用韦达定理进行快速计算。
5.使用计算器快速求解
在机考SAT数学中,Bluebook软件内置了可以全程使用、并且可以绘图的计算器,在考试中我们也可以灵活使用计算器进行快速求解。
二次方程ax2+bx+c=0的解,也可以理解成二次函数f(x)=ax2+bx+c的图像关于x轴交点的x坐标。
以2x2-5x+3=0为例 ,方程的解即为f(x)=2x2-5x+3图像与x轴交点的x坐标。我们用bluebook内置的计算器画出这个函数的图像,如下图所示,直接在计算器里输入式子,在上方会直接显示对应的函数图像,与x轴交点的x坐标即为方程的解,我们从图上可知解为x=1和x=1.5。

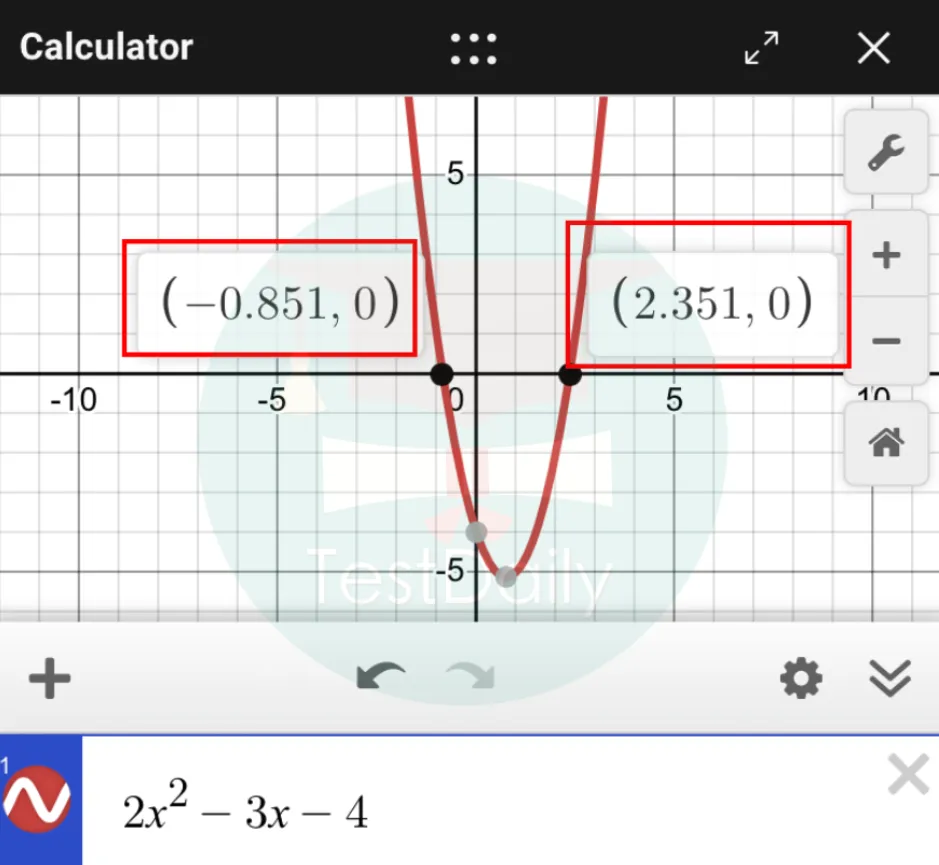
但需要注意的是,不管解是有理数还是无理数,图像上的点坐标只会保留三位小数,并不会以根式或者分数的形式出现,因此如果题目中所求的答案要求是根式或者分数的形式时,就不能用计算器画图来求得。
如前文求根公式例子中的2x2-3x-4=0,其在计算器中的图像为:
真题演练
那么在考试过程中如何选择用上述方法来解题?接下来我们来做几道题练练手~

题目的方程式a=1,且系数都为整数,首先我们可以联想到使用配方法,将式子进行配方x2-2x+1=9+1,得到(x-1)2=10,等式两边开方得到x=1+√10和x=1-√10,结合题意,k=10,选择B选项。
同时,看到题干中的这种形式,也可以想到使用求根公式来解,代入到公式中,也能快速选出k=10。
这道题用以上两种方法都能快速求解。
我们再来做一道填空题:

对于这道题,我们先把它化成常见的ax2+bx+c=0的形式,展开两边的式子后我们得到 x2+x-56=4x2-28x,然后可以得到 3x2-29x+56=0 。
因为这道题只要求求出the sum of the solutions(解的和),我们可以快速使用韦达定理得到x1+x2=-(b/a)=-(-29/3)=29/3,因此这道题的答案为29/3。
总结
一元二次方程求解有多种求解的方法,在考试中如何选用合适的方法进行求解对于做题速度和做题准确率至关重要,这非常考验同学们对公式和知识点掌握的熟练程度。
除了二次方程外,其他的知识点如指数运算公式、斜率计算公式、三角形相似、全等的条件等知识点几乎也是每次考试的必考知识,同时这些知识点都非常需要同学们熟练掌握相应的公式和知识点。
尤其是SAT机考改革后,考试实行自适应难度的模式,而对于我们中国学生来说基本第二部分都会进入到hard module,题目难、时间紧,同学们需要又快有准地完成题目。因此,在备考的过程中我们需要熟练掌握这些公式和知识点,这样才能更轻松从容地面对考试、拿下满分!
文末福利
TD SAT教研组已经为大家准备好了SAT数学必备词汇、SAT数学公式大全、Bluebook计算器使用指南以及错题整理模版,现在扫描下方二维码,添加TD小马甲的微信,并发送暗号「SAT数学」就可以领取咯~









