
在SAT数学机考中,很多知识点都不是单一出现的,可能一道题会结合多个知识点来考察同学们对知识点的熟练运用和掌握程度。今天想给大家介绍一个在advanced math部分最常跟其他知识点相结合的、也是同学们常常会忽略的一个知识点——函数图像的移动和变换(function transformations)。
SAT数学基础知识讲解
当我们对函数进行平移、拉伸、压缩和反射时,实际上在改变函数图像的位置、形状和方向。
1.平移(Translation):
平移是将函数图像沿着坐标轴的方向移动,而不改变其形状。我们可以沿着x轴或y轴方向进行平移。
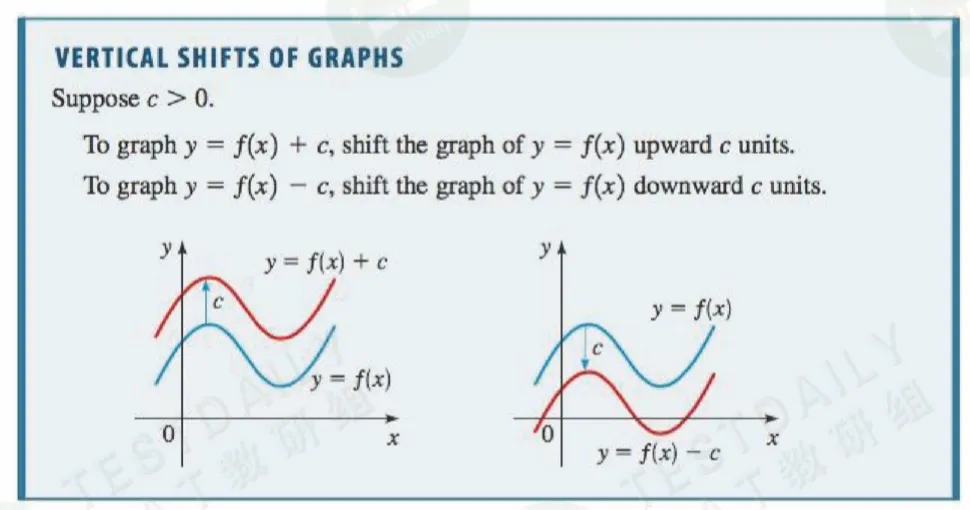
- 垂直平移:将函数图像沿y轴移动。已知函数y = f(x),若要向上移动c个单位,用y = f(x) + c表示;若要向下移动c个单位,用y = f(x) - c表示。(速记口诀:上加下减)
- 水平平移:将函数图像沿x轴移动。已知函数y = f(x),若要向右移动c个单位,用f(x - c)表示;若要向左移动c个单位,用f(x + c)表示。(速记口诀:左加右减)

2.反射(Reflection):
反射是指函数图像相关于某条坐标轴对称,从而改变函数图像的方向。
- 关于x轴的反射:函数图像在x轴上方的部分将翻转到x轴下方,反之亦然;新的图像与原图像关于x轴对称。已知函数y = f(x),关于x轴的反射用y = -f(x)表示。
- 关于y轴的反射:函数图像在y轴右侧的部分将翻转到y轴左侧,反之亦然;新的图像与原图像关于y轴对称。已知函数y = f(x),关于y轴的反射用y = f(-x)表示。

*补充知识:
拉伸和压缩在目前SAT数学考试中虽然没有考到,但是同学们可以根据自己的情况额外补充一下,在未来大学课程的学习中可能会遇到。
3.拉伸和压缩(Stretching and Compression / Scaling):
拉伸和压缩改变函数图像在水平和垂直方向上的尺寸,可以分为水平方向和垂直方向的拉伸/压缩。
- 水平伸缩:若要在水平方向对函数图像进行伸缩,可以用f(ax)表示,其中当a > 1,函数图像在水平方向压缩;当0 < a < 1,函数图像在水平方向拉伸。
- 垂直伸缩:若要在垂直方向对函数图像进行伸缩,可以用bf(x)表示,其中当b > 1,函数图像在垂直方向拉伸;当0 < b < 1,函数图像在垂直方向压缩。
example:
假设原函数是f(x)=x2,我们进行一些变换:
水平平移:f(x-2)=(x-2)2(向右平移2个单位)。
垂直平移:?f(x)+3=x2+3(向上平移3个单位)。
水平伸缩:f(2x)=(2x)2=4x2(水平压缩)。
垂直伸缩:2f(x)=2x2(垂直拉伸)。
关于 y 轴反射:?f(-x)=(-x)2=x2(x2图像关于y轴对称,因此图像不变)。
关于 x 轴反射:-f(x)=-x2(关于 x 轴反射)。
上述这些图像的平移变换可以单独使用,也可以组合使用,以便更灵活地调整函数图像。通过理解和应用这些变换,可以更好地理解和分析各种函数的行为。
SAT数学真题演练
那在SAT机考数学中,图像的平移变换会怎么跟其他知识点结合起来考呢?我们一起做一道题来感受一下~

上面这道题就是函数图像的平移变换和二次函数最大值最小值相结合的题目。如果同学们不了解函数图像的平移变换,可能会直接把(x+5)作为一个整体代入到原式f(x)中替换掉x,得到g(x)=f(x+5)=4(x+5)2+64(x+5)+262,然后再把式子展开得到一个新的二次函数再对它进行求解,但是这样就计算量非常大,在考试中非常费时间,并且也有可能因为计算错误导致算不出答案。
那我们学过图像的平移变换后就可以用图像的平移变换来做这道题:
- 求出f(x)取什么值时会达到f(x)的最小值:对于二次函数f(x),a = 4 > 0,函数图像开口向上,在f(x)的对称轴处x=-(b/2a)=-(64/8)=-8取到函数f(x)的最小值。
- g(x)=f(x+5),根据左加右减的口诀我们可以判断出函数g(x)的图像就是f(x)的图像向左平移五个单位。
- 画出新的g(x)的图像,由于图像左右水平平移y坐标的值不变,g(x)会在x = -8-5 = -13处取到它的最小值。
这样,我们就能轻松得出这道题的答案为A选项。

结语
看完上述的讲解,同学们是否掌握了这个知识点?那么在SAT机考数学的考试中,还有很多其他会互相结合出题的知识点,这就要求同学们在日常的学习过程中熟练掌握、运用学过的每一个知识点,举一反三,拓展自己的做题思路,这样才能在未来的考试中快速、准确地做题,拿到数学800的满分!
文末福利
TD SAT教研组为大家准备了机考SAT数学难题合集,现在扫描下方二维码,添加TD小马甲的微信,并发送暗号「SAT数学难题合集」就可以领取咯~








