如果说定积分、limit计算、3D-system simulation这一系列解题技巧是AMC12乃至高中数学考试披荆斩棘的“外招”的话，三角函数无疑是高中学子数学学习最重要的一项内功。 广大的美本申请者可以说在三角函数上吃尽了苦头，sat2和ap微积分还好有“人类的好帮手”-计算器可以护体，但是到了AMC12竞赛可以说大家再也逃无可逃了： TD AMC教研组总结了近年来AMC12覆盖的所有三角函数的考题，从最基本的三角函数计算到三角函数的几何意义，再到三角函数更高阶的应用，从易到难，从浅到深，考题可以说对高中能学到的所有三角函数知识点全区域覆盖，负责任地说一句：三角函数，它比想象中更重要！

2004年B卷的第18题考察的是三角函数

在几何中的应用，利用正弦函数对面积进行求解

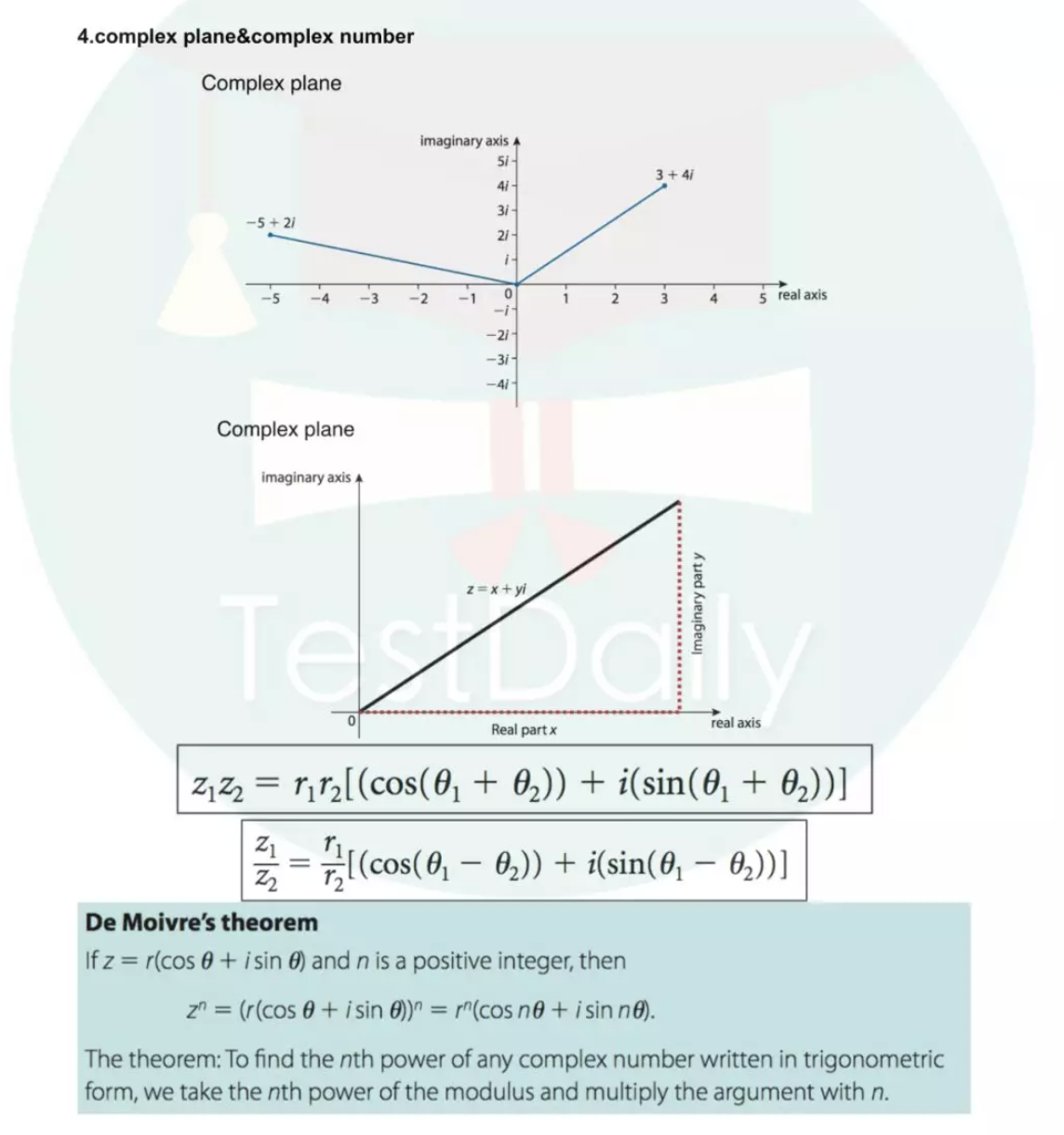
2017B卷第12题考察的是和complex plane的结合、

对roots of unity掌握的熟练程度，

以及对sin和cos在四个象限之内取值的娴熟使用

以上照片截图均出自TD的AMC12备考计划线上课内容，且仅仅是与三角函数相关的一小部分而已。 5道题的展示相信很多同学已经看到三角函数考题的跨度几乎是覆盖了它能考到的所有考点，为什么三角函数重要而又难学呢？因为它和数论-函数-几何是串在一起的，哪里都有它，哪里都靠它，内容多，逻辑线条繁杂，学扎实了数学就强得不得了，学得混乱做题常常一头雾水。 罗马不是一天建成的，三角函数也不是一天能学好的，AMC12竞赛的考期日益临近，那么我们有没有什么方法能够尽量快尽量准尽量省时间的学好三角函数或者最低限度的掌握三角函数在AMC12上的考点呢。 TD AMC教研组给同学们做了下面关于三角函数考点的总结，希望同学们都能在这份清单上逐一check，找到自己的问题，确立自己的“查漏补缺”计划，既是为了这次竞赛，也是为了在三角函数这个数学最重要的“内功”上不断进步！

1.三角函数本身

(1)unit circle（重中之重，没有之一，各个象限的对应的常见角的radian及三角函数对应取值都要能迅速反应） (2)三角函数的公式：（平方关系-倒数关系-两角和差公式-倍角公式-诱导公式） (3)三角函数自身函数名的定义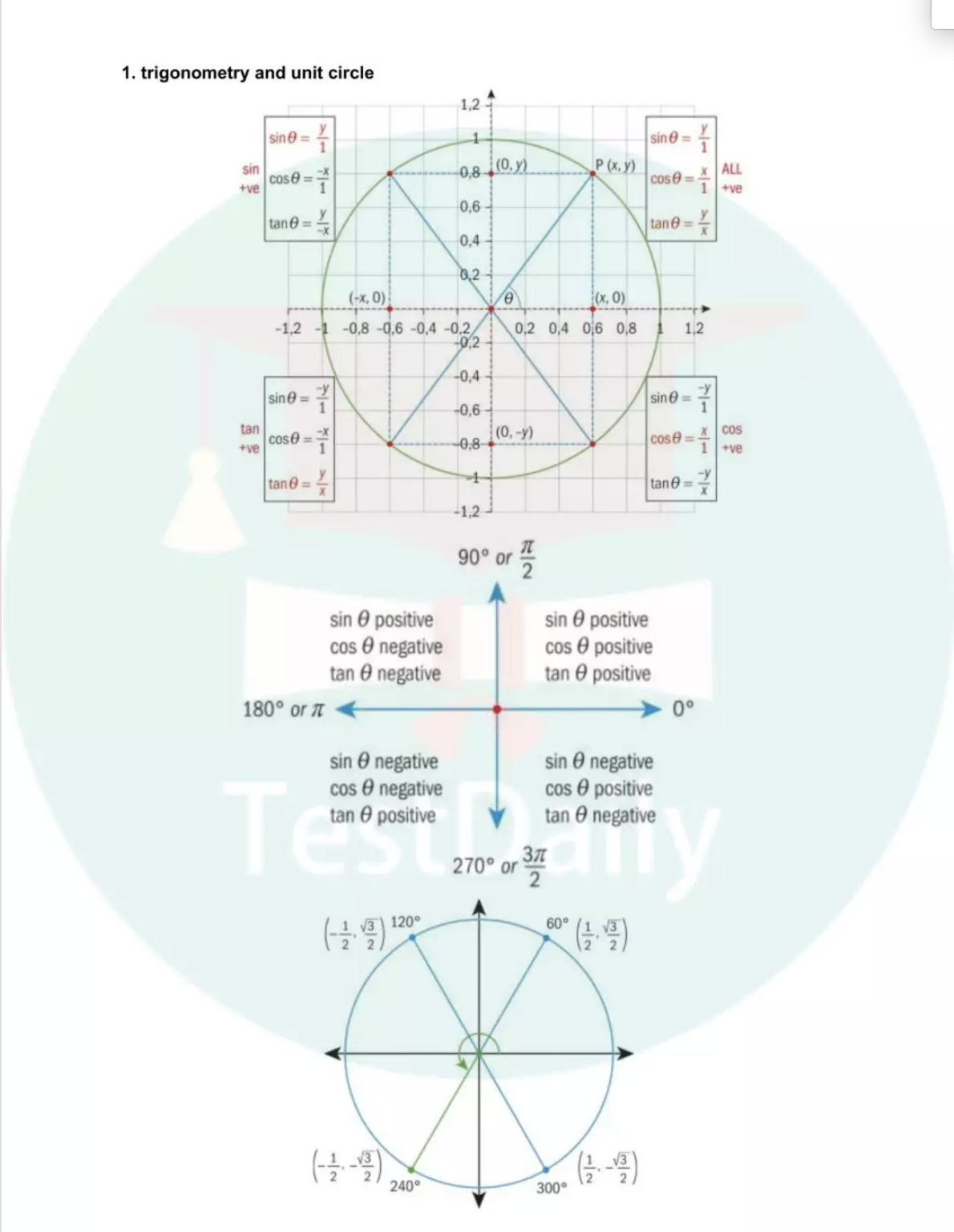

2.与函数相关 (1)三角函数的图像、周期、增减性、奇偶性、定义域、值域 (2)小部分关于三角函数的导数积分公式（选学，没有这部分知识AMC12也能做题）

3.与几何相关 (1)正余弦定理 (2)三角函数在几何图形中与面积的关系

4.与复数相关： (1)复数的三角函数表现形式 (2)熟练掌握de moivre公式以及roots of unity

AMC10/12十年真题下载

请添加客服马甲

并发送关键字「AMC真题」领取