模考AP微积分真题的时候肯定是需要离开书本,自主独立做题,要尽量在错题不增加的情况下加快速度。 至于整理错题的话,用本子记录下来,哪种类型的微积分BC题目容易错?错的原因是因为粗心还是知识点不理解?这种题型的题在AP微积分里会不会有什么引申考法?能不能从这道题联想到什么别的曾经错过的题?他们有没有什么共同点?这些都可以记下来。

比方说如果我在关于微积分极限的题目上错了,我会去想类似的题目有没有做过同样也错了的,分子分母(x-3)这里能不能像我想象的一样上下约分? 比如说虽然我这道题要去求垂直渐近线想法没错,可是是不是有两条垂直渐近线,但是我一直有一个忘记去求?
然后如果是AP微积分知识点出了问题,或者说是单词上面记录混淆,一定要及时抓住错误,这样回到框架复习的时候能知道怎样合理安排时间。
我比较喜欢的方法是先拿一张白纸针对某一个知识点想出关于它的内容,然后再回过头与书本对比看看自己有没有什么记错了的或者记少了的。 比方说这个就是我原来的一段关于黎曼求和部分的提纲整理。

这里我也拿微积分极限做个例子。 首先应该想到极限的定义:一个function在某点的极限是指自变量(input)趋近于某个数(但不是等于这个数)的时候,函数的值能无限地接近于某个确定的常数。
当然还有一层定义是自变量趋于正无穷大或者负无穷大时,AP微积分函数的值能够无限接近于某个确定的常数。 然后延伸到怎么样正确读出图像上的极限。
要学会左右极限的概念,了解到在左右极限都存在且相等的情况下,才能说明这点的极限存在。如果左右极限存在不相等那是什么情况? 然后往更加特殊的方向走,比方说什么样的极限已经有一些结论了?
e^x或者说指数函数的在自变量趋向于正无穷以及负无穷时的极限比如sinx的,自变量趋向于无穷时候的极限比如说有理函数(rational functions)的在某点的极限(要么代入,要么约了再代入,要么正无穷要么负无穷),比如说有理函数在自变量趋向于正无穷或负无穷时会怎样比如说X趋向于0,sinx/x的极限,还有我们最最最常考的洛必达法则+水平渐近线+竖直渐近线。
当然,还要搭配上自己经常错的AP微积分真题错题放在一起看,这样会加深印象。
2014AP微积分真题展示

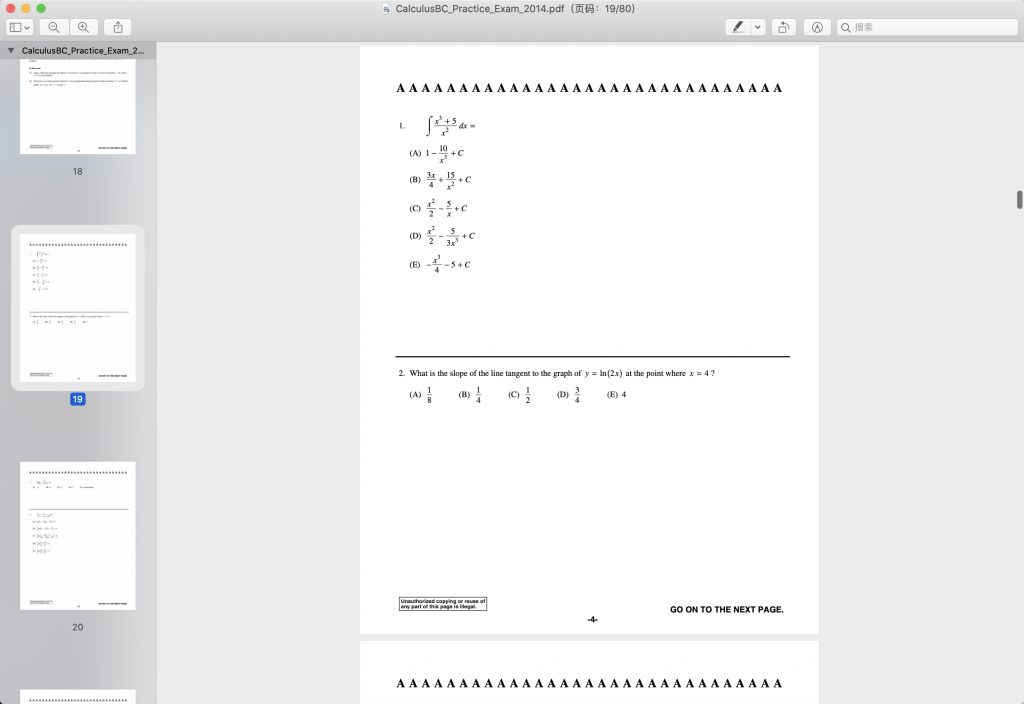
完整真题和答案获取方式:
添加客服微信并发送消息「微积分真题」,即可免费无条件领取~

[series id='361' title='TD AP网络课程' limit='5']
[series id='363' title='AP微积分真题' limit='6']




 [series id='361' title='TD AP网络课程' limit='5']
[series id='363' title='AP微积分真题' limit='6']
[series id='361' title='TD AP网络课程' limit='5']
[series id='363' title='AP微积分真题' limit='6']



 [series id='361' title='TD AP网络课程' limit='5']
[series id='363' title='AP微积分真题' limit='6']
[series id='361' title='TD AP网络课程' limit='5']
[series id='363' title='AP微积分真题' limit='6']