SAT2数学具有考试涉及面广，考察相对浅的特点。在考试中，我们会遇到很广泛的知识点，比如矩阵，向量，复数，极限等等，这些考点在每次考试中可能只出现一次，也有可能两三次考试才出现一次。但是每次出现基本都是致命的，总是伴随着较低的正确率，所以在备考SAT2数学的过程中，这些知识是极其重要的。 因为遗漏的知识点，总会成为获得满分的直接阻碍。今天带大家来盘点一下那些容易被忽视的细节考点。

矩阵(Matrix)

难度系数：★★★★ 矩阵虽然出现的频率不高，每次考试只考一个，但是它无疑是相对新颖的知识点。对于一些同学而言，这直接是一个知识盲区。 但好在矩阵在SAT2考试中只有三个考点，分别为矩阵加减，矩阵相乘以及行列式求值，考察相对浅显，所以固定掌握即可。

向量(Vector)

难度系数★★★★ 向量是特别容易被遗忘的一个知识，主要是因为向量是一个合格伪装者，当我们发现字母是粗体的时候，注意向量正在出没，所以此时就要赶快回忆起向量加减运算的规则，才能将其顺利解决。 如同上题，在向量加减运算中我们曾经学习过，两个向量的加减运算最大为二者的和，最小为二者的差，因此可以选出A选项，如果不记得这个知识点就只能乱选一通。

渐近线(Asymptote)

难度系数★★★★★ 渐近线是正经的微积分内容，即便对于很多准备AP考试的同学也总是傻傻分不清楚，对于SAT2来讲更加是一个难点。同时呢，它又很少出现，这就导致大多数同学没有机会进行充分的练习，一旦出现“死伤一片”。 渐近线和极限本来是一体的知识，但是极限可以通过计算器直接求解，这就令渐近线变成了实打实的“战地孤儿”。 所以一定要区分清楚，我们通过

寻找水平渐近线，通过

寻找垂直渐近线。

参数方程(Parametric function)

难度系数★★★ 参数方程本身实际上不算太难，即便是你没有听过参数方程，也同样可以做形如x=2t+10，y=3t+9的参数方程，我们可以通过消元法将其转换成为y=f(x)的形式。 但对于x=sin⁡θ+1，y=cos⁡θ-1这一类参数方程，总有同学忘记这类参数方程如何消参，其中部分原因也来源于三角函数部分掌握的不够清晰，对于此类参数方程，我们利用的是，将其参数消掉。

逻辑语句(Logic)

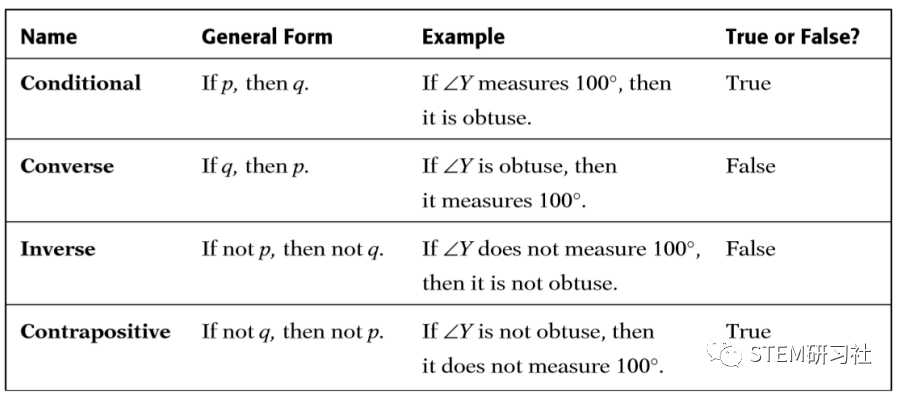
难度系数★★ 逻辑语句并不是什么难点知识，即便没有系统的接触过逻辑语句，也可以根据生活经验和数学规律反复推敲出正确的答案。但如果掌握了逻辑描述之间的关系，可以做到事半功倍，也不必再理会原文中隐含的数学知识。 掌握以下两个逻辑关系图即可，第一张为原命题（Conditional），逆命题（Converse），否命题（Inverse）以及逆否命题（Contrapositive）之间的关系，第二张为充分（sufficient）与必要（Necessary）条件之间的关系。

正态分布(Normal distribution)

难度系数★★★ 正态分布是一个听过就能做对，没听过就啥也不会的知识点。正态分布是统计学中的一个重要知识，SAT2考试仅仅要求知道它的基本图像以及图像上的特殊位置即可。其中μ为整个数据的平均值，而σ为标准差。

二项式定理(Binomial Theorem)

难度系数★★★★★ 二项式定理确实有一点儿晦涩难懂，它既是代数又是排列组合。它将我们的代数表达式和统计学知识很好的结合起来，推导过程有理有据，但如果自己推导会相对困难，所以最佳学习方式是直接记住，辨析清楚题目考察点为二项式定理即可。下式为二项式定理的通项表达： 以上七个知识点（矩阵，向量，渐近线，参数方程，逻辑语句，正态分布，二项式定理），在考试中出现的频率并不高，但造成的“伤害”却很大，往往因为对某些知识点的忽视，导致错失800分，这将非常可惜。 所以在备考过程中还是要争取做到面面俱到，只有将已知的问题都解决掉，我们才可以抵御未知的风险；只有将目标定为全部做对，考800才会犹如探囊取物。